题目内容
一船自西向东匀速航行，上午7点到达一座灯塔的南偏西75°且距灯塔80n mile的M处，若这只船的航行速度为10
n mile，则到达这座灯塔东南方向的N处是上午（ ）
| 6 |
| A、8点 | B、9点 |
| C、10点 | D、11点 |
考点：解三角形的实际应用
专题：应用题,解三角形
分析：根据题意可求得∠MPN和，∠PNM进而利用正弦定理求得MN的值，进而求得船航行的时间，即可求得问题的答案．
解答：
解：如图所示，∠MPN=75°+45°=120°，∠PNM=45°．
在△PMN中，
=
，
∴MN=
=40
，
∴t=
=
=4．
则到达这座灯塔东南方向的N处是上午7+4=11点．
故选：D．
解：如图所示，∠MPN=75°+45°=120°，∠PNM=45°．在△PMN中，
| PM |
| sin45° |
| MN |
| sin120° |
∴MN=
80×
| ||||
|
| 6 |
∴t=
| MN |
| v |
40
| ||
10
|
则到达这座灯塔东南方向的N处是上午7+4=11点．
故选：D．
点评：本题主要考查了解三角形的实际应用．解答关键是利用正弦定理建立边角关系，考查了学生分析问题和解决问题的能力，考查了转化思想．
练习册系列答案
相关题目
在△ABC中，∠A、∠B、∠C的对边分别为a、b、c，若∠A=75°，∠B=60°，c=10，则b=（ ）
A、5
| ||
B、5
| ||
C、10
| ||
D、10
|
已知奇函数f（x）为R上的减函数，则关于a的不等式f（a2）+f（2a）＞0的解集是（ ）
| A、（-2，0 ） |
| B、（ 0，2 ） |
| C、（-2，0 ）∪（ 0，2 ） |
| D、（-∞，-2 ）∪（ 0，+∞） |
已知集合A={x|x（x-1）≤0，x∈R}，B={x|-2＜x＜1，x∈R}，那么集合A∩B是（ ）
| A、{x|-2＜x≤1，x∈R} |
| B、{x|0≤x＜1，x∈R} |
| C、{x|0＜x≤1，x∈R} |
| D、{x|0＜x＜1，x∈R} |
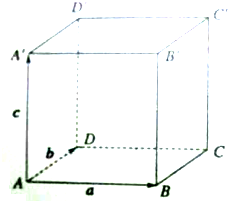已知正方体ABCD-A′B′C′D′的棱长为1，设