题目内容
14.已知抛物线y2=4$\sqrt{3}$x的准线与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1两条渐近线分别交于A,B两点,且|AB|=2,则双曲线的离心率e为$\frac{2\sqrt{3}}{3}$.分析 由已知条件,分别求出抛物线的准线方程和双曲线的渐近线,由|AB|=2,求出b=$\frac{\sqrt{3}}{3}$a,由此能求出双曲线的离心率.
解答 解:y2=4$\sqrt{3}$x的准线方程为l:x=-$\sqrt{3}$,
双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两条渐近线分别为:y=±$\frac{b}{a}$x,
∵抛物线y2=4$\sqrt{3}$x的准线与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1两条渐近线分别交于A,B两点,且|AB|=2,
∴$\frac{2\sqrt{3}b}{a}$=2
即b=$\frac{\sqrt{3}}{3}$a,
∴c=$\frac{2\sqrt{3}}{3}$a,
∴e=$\frac{c}{a}$=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查双曲线的离心率的求法,是中档题,解题时要熟练掌握抛物线、双曲线的简单性质.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
4.某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如2×2下列联表:
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数X,试求随机变量X的分布列和数学期望;
(2)若在犯错误的概率不超过P的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的P的值应为多少?请说明理由.
附:独立性检验统计量${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
独立性检验临界值表:
| 做不到科学用眼 | 能做到科学用眼 | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 合计 | 75 | 25 | 100 |
(2)若在犯错误的概率不超过P的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的P的值应为多少?请说明理由.
附:独立性检验统计量${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
独立性检验临界值表:
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
5.设f′(x)为函数f(x)的导函数,已知x2f′(x)+xf(x)=lnx,f(1)=$\frac{1}{2}$,则下列结论正确的是( )
| A. | f(x)在(0,+∞)上有极大值$\frac{1}{2}$ | B. | f(x)在(0,+∞)上有极小值$\frac{1}{2}$ | ||
| C. | f(x)在(0,+∞)单调递增 | D. | f(x)在(0,+∞)单调递减 |
19.设函数f(x)是定义在R上的奇函数,当x∈(0,1]时f(x)=1+log2x.若对任意的x∈R都有f(x)=f(x+4),则f(2014)+f(2016)-2f(2015)=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
6.对于直线m,n和平面α,β,能得出α⊥β的一个条件是( )
| A. | m⊥n,m∥α,n∥β | B. | m⊥n,α∩β=m,n?α | C. | m∥n,n⊥β,m?α | D. | m∥n,m⊥α,n⊥β |
4.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为( )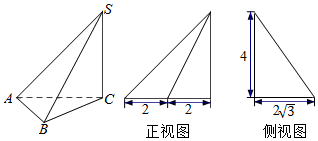

| A. | $16\sqrt{3}$ | B. | $\sqrt{38}$ | C. | $4\sqrt{2}$ | D. | $2\sqrt{11}$ |
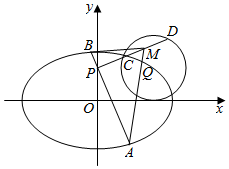 已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F2在以$Q(\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.
已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F2在以$Q(\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.