题目内容
19.设函数f(x)是定义在R上的奇函数,当x∈(0,1]时f(x)=1+log2x.若对任意的x∈R都有f(x)=f(x+4),则f(2014)+f(2016)-2f(2015)=( )| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
分析 由f(x)=f(x+4)得出f(x)是周期为4的函数,再由f(x)是奇函数,求出f(2)=f(-2)=0,从而求出f(2015)与f(2014)、f(2016)的值.
解答 解:∵f(x)=f(x+4),∴f(-2)=f(-2+4)=f(2),
又∵奇函数f(x),∴f(-2)=-f(2)=0,
又∵2015=4•504-1,2014=4•503+2,2016=4•504,
∴f(2015)=f(-1)=-1,f(2014)=f(2)=0,f(2016)=0
∴f(2014)+f(2016)-2f(2015)=2.
故选:D.
点评 本题考查了函数的奇偶性和周期性的应用问题,是基础题目.

练习册系列答案
相关题目
9.已知函数f(x)=sin(ωx+φ)(ω>0)的图象如图所示,则f($\frac{5π}{6}$)=( )
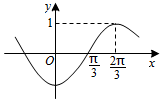

| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
10.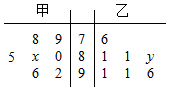 某中学从甲、乙两个艺术班中各选出7名同学参加才艺比赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班同学成绩的众数是80,乙班同学成绩的中位数是88,则x+y的值为( )
某中学从甲、乙两个艺术班中各选出7名同学参加才艺比赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班同学成绩的众数是80,乙班同学成绩的中位数是88,则x+y的值为( )
 某中学从甲、乙两个艺术班中各选出7名同学参加才艺比赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班同学成绩的众数是80,乙班同学成绩的中位数是88,则x+y的值为( )
某中学从甲、乙两个艺术班中各选出7名同学参加才艺比赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班同学成绩的众数是80,乙班同学成绩的中位数是88,则x+y的值为( )| A. | 11 | B. | 9 | C. | 8 | D. | 3 |
11.已知一个算法的程序图如图所示,当输入x∈[-2,9]时,则输出的y属于( )


| A. | [-1,2] | B. | [0,2] | C. | [-1,$\frac{5}{2}$) | D. | [0,$\frac{5}{2}$) |
8.若复数z满足(2+i)z=|1-2i|,则复数z所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |