题目内容

4．三棱锥S-ABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为（　　）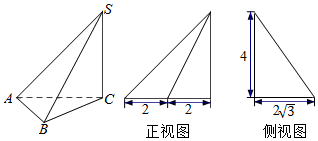
A．$16\sqrt{3}$B．$\sqrt{38}$C．$4\sqrt{2}$D．$2\sqrt{11}$

分析 根据三视图得SC⊥平面ABC，且底面△ABC为等腰三角形，根据图中数据与勾股定理求出SB的值．

解答 解：由已知中的三视图可得SC⊥平面ABC，且底面△ABC为等腰三角形，
在△ABC中，AC=4，AC边上的高为$2\sqrt{3}$，
所以BC=4；
在Rt△SBC中，由SC=4，可得SB=$4\sqrt{2}$．
故选：C．

点评 本题考查了空间几何体三视图的应用问题，也考查了空间中的垂直关系的应用问题，是基础题．

练习册系列答案
相关题目
14．已知抛物线y2=4$\sqrt{3}$x的准线与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1两条渐近线分别交于A，B两点，且|AB|=2，则双曲线的离心率e为$\frac{2\sqrt{3}}{3}$．
15．函数$f（x）=\frac{b}{|x|-a}（a＞0，b＞0）$的图象形如汉字“囧”，故称其为“囧函数”．下列命题：
①“囧函数”的值域为R；
②“囧函数”在（0，+∞）上单调递增；
③“囧函数”的图象关于y轴对称；
④“囧函数”有两个零点；
⑤“囧函数”的图象与直线y=kx+m（k≠0）至少有一个交点．
正确命题的个数为（　　）
A．1B．2C．3D．4
12．已知函数f（x）=4x+$\frac{a}{x}$（x＞0，a＞0）在x=2时取得最小值，则实数a=16．
19．设函数f（x）=exlnx+$\frac{2{e}^{x-1}}{x}$，证明f（x）＞1．
9．在平面直角坐标系xOy中，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦距为2．
（1）若椭圆C经过点（$\frac{\sqrt{6}}{2}$，1），求椭圆C的标准方程；
（2）设A（-2，0），F为椭圆C的左焦点，若椭圆C上存在点P，满足$\frac{PA}{PF}$=$\sqrt{2}$，求椭圆C的离心率的取值范围．
16．若a=$\frac{1-cosα}{sinα}$，b=$\frac{1+cosα}{sinα}$，则ab的值是（　　）
A．0B．1C．-1D．$\sqrt{2}$
13．若函数f（x）是奇函数．且在x＞0时是增函数，则下列结论中正确的是（　　）
A．f（-1）＜f（-2）＜f（-3）B．f（-3）＜f（-2）＜f（-1）C．f（-2）＜f（-1）＜f（-3）D．f（-3）＜f（-1）＜f（-2）
14．已知函数g（x）=（$\frac{1}{2}$）|x-1|，则r=g（2-0.1），s=g（log0.23），t=g（2），则r，s，t的大小关系是（　　）
A．t＜r＜sB．t＜s＜rC．s＜r＜tD．s＜t＜r

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网