题目内容
9.已知正项数列{an}满足,a1=1,an+1=$\frac{{a}_{n}}{2{a}_{n}+1}$(n∈N+).(1)证明数列{$\frac{1}{{a}_{n}}$}为等差数列,并求数列{an}的通项公式;
(2)设bn=(-1)n•n•an•an+1,求数列{bn}的前n项和Tn.
分析 (1)a1=1,an+1=$\frac{{a}_{n}}{2{a}_{n}+1}$(n∈N+),两边取倒数可得$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=2,即可证明,再利用等差数列的通项公式即可得出.
(2)bn=(-1)n•n•an•an+1=(-1)nn$•\frac{1}{(2n-1)(2n+1)}$=$(-1)^{n}•\frac{1}{4}$$(\frac{1}{2n-1}+\frac{1}{2n+1})$.对n分类讨论即可得出.
解答 (1)证明:∵a1=1,an+1=$\frac{{a}_{n}}{2{a}_{n}+1}$(n∈N+),两边取倒数可得$\frac{1}{{a}_{n+1}}$=2+$\frac{1}{{a}_{n}}$,即$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=2,
∴数列{$\frac{1}{{a}_{n}}$}为等差数列,首项为1,公差为2.
∴$\frac{1}{{a}_{n}}$=1+2(n-1)=2n-1,解得an=$\frac{1}{2n-1}$.
(2)解:bn=(-1)n•n•an•an+1=(-1)nn$•\frac{1}{(2n-1)(2n+1)}$=$(-1)^{n}•\frac{1}{4}$$(\frac{1}{2n-1}+\frac{1}{2n+1})$.
∴n=2k(k∈N*),数列{bn}的前n项和Tn=T2k=$\frac{1}{4}$$[-(1+\frac{1}{3})+(\frac{1}{3}+\frac{1}{5})$-$(\frac{1}{5}+\frac{1}{7})$+…-$(\frac{1}{2n-3}+\frac{1}{2n-1})$+$(\frac{1}{2n-1}+\frac{1}{2n+1})]$
=$\frac{1}{4}$$(-1+\frac{1}{2n+1})$=$\frac{-n}{4n+2}$.
n=2k-1(k∈N*),数列{bn}的前n项和Tn=T2k-1=$\frac{1}{4}$$[-(1+\frac{1}{3})+(\frac{1}{3}+\frac{1}{5})$-$(\frac{1}{5}+\frac{1}{7})$+…+$(\frac{1}{2n-3}+\frac{1}{2n-1})$-$(\frac{1}{2n-1}+\frac{1}{2n+1})]$
=$\frac{1}{4}$$(-1-\frac{1}{2n+1})$=-$\frac{n+1}{4n+2}$.
综上可得:Tn=$\left\{\begin{array}{l}{\frac{-n}{4n+2},n=2k}\\{\frac{-(n+1)}{4n+2},n=2k-1}\end{array}\right.$(k∈N*).
点评 本题考查了数列递推关系、等差数列的定义与通项公式、“裂项求和”方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.

| A. | cosβ=2cosα | B. | cos2β=2cos2α | C. | cos2β=2cos2α | D. | cos2β=-2cos2α |
| A. | $\sqrt{3}$akm | B. | 2akm | C. | $\sqrt{5}$akm | D. | $\sqrt{7}$akm |
| A. | (1,+∞) | B. | $(1,1+\sqrt{2})$ | C. | $(1,\sqrt{3})$ | D. | $(1-\sqrt{2},1+\sqrt{2})$ |
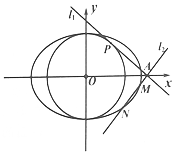 已知椭圆C:$\frac{{x}^{2}}{2}+{y}^{2}=1$和圆O:x2+y2=1,过点A(m,0)(m>1)作两条互相垂直的直线l1,l2,l1于圆O相切于点P,l2与椭圆相交于不同的两点M,N.
已知椭圆C:$\frac{{x}^{2}}{2}+{y}^{2}=1$和圆O:x2+y2=1,过点A(m,0)(m>1)作两条互相垂直的直线l1,l2,l1于圆O相切于点P,l2与椭圆相交于不同的两点M,N.