题目内容
13.已知圆C:(x-m)2+(y-n)2=9的圆心在第一象限,直线l:x+2y+2=0与圆C相交的弦长为4,则$\frac{m+2n}{mn}$的最小值为$\frac{8}{3}$.分析 根据直线和圆相交的弦长公式,求出m,n的关系,结合基本不等式进行求解即可.
解答 解:圆心C(m,n),半径R=3,
∵圆心在第一象限,
∴m>0,n>0.
∵直线l:x+2y+2=0与圆C相交的弦长为4,
∴圆心到直线的距离d=$\sqrt{{R}^{2}-{2}^{2}}=\sqrt{9-4}$=$\sqrt{5}$,
即$\frac{|m+2n+2|}{\sqrt{5}}=\sqrt{5}$,即m+2n+2=5,
则m+2n=3,即$\frac{m}{3}$+$\frac{2n}{3}$=1,
则$\frac{m+2n}{mn}$=($\frac{1}{n}$+$\frac{2}{m}$)×($\frac{m}{3}$+$\frac{2n}{3}$)=$\frac{2}{3}$+$\frac{2}{3}$+$\frac{m}{3n}$+$\frac{4n}{3m}$≥$\frac{4}{3}$+2$•\sqrt{\frac{m}{3n}•\frac{4n}{3m}}$=$\frac{4}{3}+\frac{4}{3}$=$\frac{8}{3}$,
当且仅当$\frac{m}{3n}$=$\frac{4n}{3m}$,即m=2n时取等号,
故答案为:$\frac{8}{3}$.
点评 本题主要考查基本不等式的应用,根据直线与圆相交的性质,利用1的代换是解决本题的关键.

练习册系列答案
相关题目
8.已知全集为R,且A={x|log2(x+1)<2},B={x|$\frac{x-2}{x-1}$≥0},则A∩(∁RB)等于( )
| A. | (-1,1) | B. | (-1,1] | C. | [1,2] | D. | [1,2) |
5.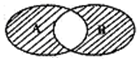 如图所示的韦恩图中,A、B是非空集合,定义A*B表示阴影部分的集合.若x,y∈R,A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=3x,x>0}.则A*B为( )
如图所示的韦恩图中,A、B是非空集合,定义A*B表示阴影部分的集合.若x,y∈R,A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=3x,x>0}.则A*B为( )
 如图所示的韦恩图中,A、B是非空集合,定义A*B表示阴影部分的集合.若x,y∈R,A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=3x,x>0}.则A*B为( )
如图所示的韦恩图中,A、B是非空集合,定义A*B表示阴影部分的集合.若x,y∈R,A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=3x,x>0}.则A*B为( )| A. | {x|0<x<2} | B. | {x|1<x≤2} | C. | {x|0≤x≤1或x≥2} | D. | {x|0≤x≤1或x>2} |
17.函数f(x)=x-sinx(x∈R),则f(x)( )
| A. | 是奇函数,且在(-∞,+∞)上是减函数 | B. | 是偶函数,且在(-∞,+∞)上是减函数 | ||
| C. | 是偶函数,且在(-∞,+∞)上是增函数 | D. | 是奇函数,且在(-∞,+∞)上是增函数 |
 如果执行右边的程序框图,输出的值为x,则${x}^{\frac{1}{2}}$+log3x=5.
如果执行右边的程序框图,输出的值为x,则${x}^{\frac{1}{2}}$+log3x=5.