题目内容
18.设(a+i)2=bi,其中a,b均为实数,若z=a+bi,则|z|=$\sqrt{5}$.分析 利用复数的运算法则、复数相等、模的计算公式即可得出.
解答 解:bi=(a+i)2=a2-1+2ai,其中a,b均为实数,
∴a2-1=0,b=2a.
a=1,b=2,或a=-1,b=-2.
若z=a+bi,则|z|=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查了复数的运算法则、复数相等、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
9.已知x,y,z为正实数,则$\frac{xy+yz}{{x}^{2}+{y}^{2}+{z}^{2}}$的最大值为( )
| A. | $\frac{2\sqrt{3}}{5}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
6.把函数f(x)=cos(2x+φ)的图象上所有的点向左平移$\frac{π}{6}$个单位长度后得到y=g(x)的图象,若y=g(x)的一个对称中心是($\frac{π}{6}$,0),则φ的一个可能取值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{7π}{12}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
2.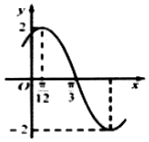 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将f(x)图象上所有点向右平移$\frac{π}{12}$个单位得到函数g(x)的图象,则函数g(x)的单调递减区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将f(x)图象上所有点向右平移$\frac{π}{12}$个单位得到函数g(x)的图象,则函数g(x)的单调递减区间为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将f(x)图象上所有点向右平移$\frac{π}{12}$个单位得到函数g(x)的图象,则函数g(x)的单调递减区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将f(x)图象上所有点向右平移$\frac{π}{12}$个单位得到函数g(x)的图象,则函数g(x)的单调递减区间为( )| A. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z | B. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z | ||
| C. | [kπ-$\frac{π}{12}$,kπ+$\frac{π}{12}$],k∈Z | D. | [kπ-$\frac{7π}{12}$,kπ-$\frac{π}{12}$],k∈Z |
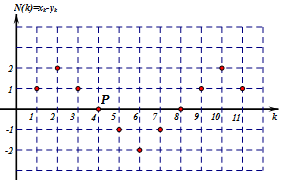 已知一个由11人组成的评审委员会以投票方式从符合要求的甲,乙两名候选人中选出一人参加一次活动.投票要求委员会每人只能选一人且不能弃选,每位委员投票不受他人影响.投票结果由一人唱票,一人统计投票结果.
已知一个由11人组成的评审委员会以投票方式从符合要求的甲,乙两名候选人中选出一人参加一次活动.投票要求委员会每人只能选一人且不能弃选,每位委员投票不受他人影响.投票结果由一人唱票,一人统计投票结果.