题目内容
11.二项式${({\sqrt{x}+\frac{1}{{{\;}^4\sqrt{x}}}})^8}$的展开式中含x项的系数为70.分析 利用二项式展开式的通项公式,令x项的指数为1求出r的值,再计算含x项的系数.
解答 解:二项式${({\sqrt{x}+\frac{1}{{{\;}^4\sqrt{x}}}})^8}$的展开式中,
通项公式为Tr+1=${C}_{8}^{r}$•${(\sqrt{x})}^{8-r}$•${(\frac{1}{\root{4}{x}})}^{r}$=${C}_{8}^{r}$•${x}^{4-\frac{3r}{4}}$,
令4-$\frac{3r}{4}$=1,解得r=4;
所以展开式中含x项的系数为${C}_{8}^{4}$=70.
故答案为:70.
点评 本题考查了二项式展开式通项公式的应用问题,是基础题目.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
1.运行如图所示的程序框图,输出的结果S=( )


| A. | 14 | B. | 30 | C. | 62 | D. | 126 |
19.如图是用二分法求方程x3-2=0近似解的算法的程序框图,则①②两处应依次填入( )


| A. | a=m,b=m | B. | b=m,a=m | C. | a=f(m),b=f(m) | D. | b=f(m),a=f(m) |
16.有两位射击运动员在一次射击测试中各射靶7次,每次命中的环数如下:
甲 7 8 10 9 8 8 6
乙 9 10 7 8 7 7 8
则下列判断正确的是( )
甲 7 8 10 9 8 8 6
乙 9 10 7 8 7 7 8
则下列判断正确的是( )
| A. | 甲射击的平均成绩比乙好 | |
| B. | 乙射击的平均成绩比甲好 | |
| C. | 甲射击的成绩的众数小于乙射击的成绩的众数 | |
| D. | 甲射击的成绩的极差大于乙射击的成绩的极差 |
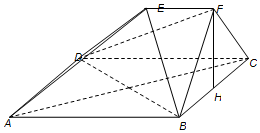 如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,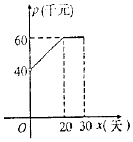 根据市场调查,某种新产品投放市场的30天内,每件的销售价格p(千元)与时间x(天)组成有序数对(x,p),点(x,p)落在下图中的两条线段上,且日销售量q(件)与时间x(天)之间的关系是q=-x+60(x∈N*).
根据市场调查,某种新产品投放市场的30天内,每件的销售价格p(千元)与时间x(天)组成有序数对(x,p),点(x,p)落在下图中的两条线段上,且日销售量q(件)与时间x(天)之间的关系是q=-x+60(x∈N*).