题目内容
1.已知函数f(x)=$\sqrt{\frac{2-x}{3+x}}+ln({{3^x}-\frac{1}{3}})$的定义域为M.(1)求M;
(2)当x∈M时,求$g(x)={4^{x+\frac{1}{2}}}-{2^{x+2}}$+1的值域.
分析 (1)根据函数f(x)有意义,可得$\left\{\begin{array}{l}\frac{2-x}{3+x}≥0\\{3^x}-\frac{1}{3}>0\end{array}\right.$,解出x的范围可得定义域M.
(2)讲g(x)化简,转化为二次函数的问题,利用x∈M时,考查单调性可得值域.
解答 解:(1)由已知可得$\left\{\begin{array}{l}\frac{2-x}{3+x}≥0\\{3^x}-\frac{1}{3}>0\end{array}\right.⇒\left\{\begin{array}{l}-3<x≤2\\ x>-1\end{array}\right.$,
∴-1<x≤2,
所以M=(-1,2].
(2)由$g(x)={4^{x+\frac{1}{2}}}-{2^{x+2}}+1=2•{2^{2x}}+4•{2^x}+1=2{({{2^x}-1})^2}-1$,
∵x∈M,即-1<x≤2,
∴$\frac{1}{2}<{2^x}<4$,
∴当2x=1,即x=0时,g(x)min=-1,
当2x=4,即x=2时,g(x)max=17,
故得g(x)的值域为[-1,17].
点评 本题考查定义域的求法和指数函数的化简能力,转化思想,利用二次函数和指数的性质的单调性求解值域,属于函数函数性质应用题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
16.函数$f(x)=({1-\frac{2}{{1+{2^x}}}})tanx$的图象( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于y=x轴对称 | D. | 关于原点轴对称 |
10.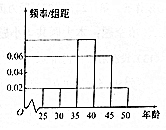 某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
下面是年龄的分布表
(1)求正整数a、b、N的值;
(2)现要从年龄低于40岁的员工中用分层抽样的方法抽取42人,则年龄在第1、2、3组的员工人数分别是多少?
(3)为了估计该单位员工的阅读习惯,对第1、2、3组中抽出的42人是否喜欢阅读国学类书籍进行了调查,调查结果如表所示:(单位:人)
根据表中数据,能否在犯错误的概率不超过0.5%的前提下认为该单位员工“是否喜欢阅读国学类书籍和性别有关系”?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
 某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.下面是年龄的分布表
| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) |
| 人数 | 28 | a | b |
(2)现要从年龄低于40岁的员工中用分层抽样的方法抽取42人,则年龄在第1、2、3组的员工人数分别是多少?
(3)为了估计该单位员工的阅读习惯,对第1、2、3组中抽出的42人是否喜欢阅读国学类书籍进行了调查,调查结果如表所示:(单位:人)
| 喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
| 男 | 16 | 4 | 20 |
| 女 | 8 | 14 | 22 |
| 合计 | 24 | 18 | 42 |
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
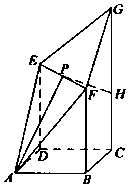 如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,DE=BF=$\frac{3}{5}$CG.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得GH=$\frac{3}{5}$CG.
如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,DE=BF=$\frac{3}{5}$CG.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得GH=$\frac{3}{5}$CG.