题目内容
6.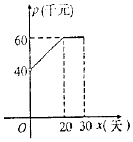 根据市场调查,某种新产品投放市场的30天内,每件的销售价格p(千元)与时间x(天)组成有序数对(x,p),点(x,p)落在下图中的两条线段上,且日销售量q(件)与时间x(天)之间的关系是q=-x+60(x∈N*).
根据市场调查,某种新产品投放市场的30天内,每件的销售价格p(千元)与时间x(天)组成有序数对(x,p),点(x,p)落在下图中的两条线段上,且日销售量q(件)与时间x(天)之间的关系是q=-x+60(x∈N*).(Ⅰ) 写出该产品每件销售价格p〔千元)与时间x(天)之间的函数关系式;
(Ⅱ) 在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品的销售价格×日销售量)
分析 (Ⅰ) 根据已知条件,利用分段函数写出该产品每件销售价格p〔千元)与时间x(天)之间的函数关系式;
(Ⅱ)利用分段函数通过二次函数以及函数的单调性分别求解最值,推出结果即可.
解答 解:(Ⅰ)根据图象,每件的销售价格p与时间x的函数关系为:$p=\left\{\begin{array}{l}{x+400(0<x≤20,x∈{N}^{•})}\\{60(20<x≤30,x∈{N}^{•})}\end{array}\right.$,
(Ⅱ)设第x天的日销售金额为y(千元),则y=$\left\{\begin{array}{l}{(x+40)(-x+60),(0<x≤20,x∈{N}^{•})}\\{60(60-x),(20<x≤30,x∈{N}^{•})}\end{array}\right.$,
即y=$\left\{\begin{array}{l}{-{x}^{2}+20x+2400,0<x≤20,x∈{N}^{•}}\\{-60x+3600,20<x≤30,x∈{N}^{•}}\end{array}\right.$.
当0<x≤20,x∈N*时,y=-x2+20x+2400=-(x-10)2+2500,∴当x=10时,ymax=2500,
当20<x≤30,x∈N*时,y=-60x+3600是减函数,∴y<-60×20+3600=2400,
因此,这种产品在第10天的日销售金额最大.
点评 本题考查函数的实际应用,分段函数的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
18.已知m,n为两条直线,α,β为两个不同的平面,则下列说法正确的是( )
| A. | 若m∥α,α∥β,则m∥β | B. | 若α⊥β,m?α,则m⊥β | ||
| C. | 若m⊥α,m∥n,α⊥β,则n∥β | D. | 若m⊥α,m∥n,α∥β,则n⊥β |
16.函数$f(x)=({1-\frac{2}{{1+{2^x}}}})tanx$的图象( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于y=x轴对称 | D. | 关于原点轴对称 |
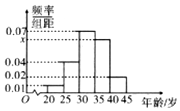 为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.
为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.
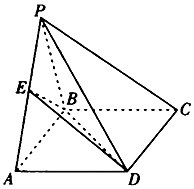 如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中点,且PA=PB=AB=4,$BC=\sqrt{2}$.
如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中点,且PA=PB=AB=4,$BC=\sqrt{2}$.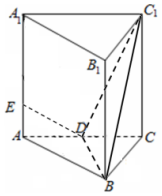 已知正三棱柱ABC-A1B1C1中,AB=AA1=2,点D为AC的中点,点E为AA1上.
已知正三棱柱ABC-A1B1C1中,AB=AA1=2,点D为AC的中点,点E为AA1上.