题目内容
16.有两位射击运动员在一次射击测试中各射靶7次,每次命中的环数如下:甲 7 8 10 9 8 8 6
乙 9 10 7 8 7 7 8
则下列判断正确的是( )
| A. | 甲射击的平均成绩比乙好 | |
| B. | 乙射击的平均成绩比甲好 | |
| C. | 甲射击的成绩的众数小于乙射击的成绩的众数 | |
| D. | 甲射击的成绩的极差大于乙射击的成绩的极差 |
分析 分别求出甲、乙命中的环数的平均数、众数、极差,由此能求出结果.
解答 解:甲命中的环数的平均数为:
$\overline{{x}_{甲}}$=$\frac{1}{7}$(7+8+10+9+8+8+6)=8,
乙命中的环数的平均数为:
$\overline{{x}_{乙}}$=$\frac{1}{7}$(9+10+7+8+7+7+8)=8,
∴甲、乙射击的平均成绩相等,故A,B均错误;
甲射击的成绩的众数是8,乙射击的成绩的众数是7,
∴甲射击的成绩的众数大于乙射击的成绩的众数,故C错误;
甲射击的成绩的极差为10-6=4,乙射击的成绩的极差为10-7=3,
∴甲射击的成绩的极差大于乙射击的成绩的极差,
故D正确.
点评 本题考查平均数、众数、极差的求法及应用,是基础题,解题时要认真审题,注意等平均数、众数、极差的定义的合理运用.

练习册系列答案
相关题目
7.已知实数x,y满足ax<ay(0<a<1),则下列关系式恒成立的是( )
| A. | $\frac{1}{{{x^2}+1}}>\frac{1}{{{y^2}+1}}$ | B. | ln(x2+1)>ln(y2+1) | C. | sinx>siny | D. | x3>y3 |
5.已知3∈{1,a,a-2},则实数a的值为( )
| A. | 3 | B. | 5 | C. | 3或 5 | D. | 无解 |
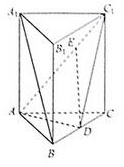 在正三棱柱ABC-A1B1C1中,点D为BC的中点;
在正三棱柱ABC-A1B1C1中,点D为BC的中点;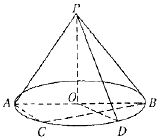 如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.
如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.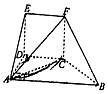 如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.
如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.