题目内容
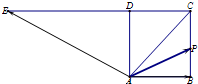如图，四边形ABCD是边长为1的正方形，延长CD至E，使得DE=2CD．动点P从点A出发，沿正方形的边按逆时针方向运动一周回到A点，| AP |
| AB |
| AE |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：分别讨论点P在线段AB，BC，CD，DA上，利用共线向量基本定理用向量
，
来表示向量
．在这一过程可以出现参数k，并且知道k的取值范围，所以根据平面向量基本定理可用k表示λ+μ，由k的范围从而求出λ+μ的范围，对在这四种情况下求得的λ+μ的范围求并集即可．
| AB |
| AE |
| AP |
解答：
解：①当P点在线段AB上时，
=λ
，0≤λ≤1；
∴0≤λ+μ≤1；
②当P点在线段BC上时，∵
=
+
=
+2
；
∴
=
+
=
+k
=（1+2k）
+k
，0＜k≤1；
∴λ+μ=1+2k+k=1+3k，1＜1+3k≤4；
∴1＜λ+μ≤4；
③当P在线段CD上时，
=
+
=
+2
+k
=(2+k)
+
，0＜k≤1；
∴λ+μ=3+k，3＜k≤4；
∴3＜λ+μ≤4；
④当P在线段AD上时，
=k
=k
+2k
，0＜k＜1；
∴λ+μ=3k，0＜3k＜3；
∴0＜λ+μ＜3；
∴综上得0≤λ+μ≤4；
∴λ+μ的取值范围为[0，4]．
故答案为[0，4]．
| AP |
| AB |
∴0≤λ+μ≤1；
②当P点在线段BC上时，∵
| AD |
| AE |
| ED |
| AE |
| AB |
∴
| AP |
| AB |
| BP |
| AB |
| AD |
| AB |
| AE |
∴λ+μ=1+2k+k=1+3k，1＜1+3k≤4；
∴1＜λ+μ≤4；
③当P在线段CD上时，
| AP |
| AD |
| DP |
| AE |
| AB |
| AB |
| AB |
| AE |
∴λ+μ=3+k，3＜k≤4；
∴3＜λ+μ≤4；
④当P在线段AD上时，
| AP |
| AD |
| AE |
| AB |
∴λ+μ=3k，0＜3k＜3；
∴0＜λ+μ＜3；
∴综上得0≤λ+μ≤4；
∴λ+μ的取值范围为[0，4]．
故答案为[0，4]．
点评：考查向量的加法，以及共线向量基本定理，平面向量基本定理．
练习册系列答案
考前必练系列答案
相关题目
曲线
+
=1(a＜6)与曲线
+
=1（5＜b＜9）有（ ）
| x2 |
| 10-a |
| y2 |
| 6-a |
| x2 |
| 5-b |
| y2 |
| 9-b |
| A、相同的离心率 |
| B、相同的准线 |
| C、相同的焦点 |
| D、相同的焦距 |
已知实数a，b满足a＜b，则下列结论正确的是（ ）
A、
| ||||
| B、2a＞2b | ||||
| C、lna＜lnb | ||||
| D、a3＜b3 |
若某几何体的三视图 （单位：cm） 如图所示，则此几何体的体积是（ ）
| A、36 cm3 |
| B、48 cm3 |
| C、60 cm3 |
| D、72 cm3 |
为确保信息安全，信息需加密传输，发送方由明文→密文（加密），已知加密规则如图所示，求明文1，2，3，4对应密文