题目内容
经过原点（0，0）做函数f（x）=x3+2x2的切线，则切线方程为 ．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出函数的导数，利用导数的几何意义：切点处的导数值是切线的斜率，分原点是切点和原点不是切点两类求．
解答：
解f′（x）=3x2+4．设切线的斜率为k．
（1）当切点是原点时k=f′（0）=4，
所以所求曲线的切线方程为y=4x．
（2）当切点不是原点时，设切点是（x0，y0），
则有y0=x03+2x02，k=f′（x0）=3x02+4，①
又k=
=x02+2x0，②
由①②得方程组无解，故曲线的切线方程是y=4x；
故答案为：y=4x．
（1）当切点是原点时k=f′（0）=4，
所以所求曲线的切线方程为y=4x．
（2）当切点不是原点时，设切点是（x0，y0），
则有y0=x03+2x02，k=f′（x0）=3x02+4，①
又k=
| y0 |
| x0 |
由①②得方程组无解，故曲线的切线方程是y=4x；
故答案为：y=4x．
点评：本题考查导数的几何意义：切点处的导数值是切线的斜率；注意“在点处的切线”与“过点的切线”的区别．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
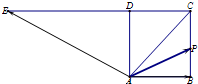如图，四边形ABCD是边长为1的正方形，延长CD至E，使得DE=2CD．动点P从点A出发，沿正方形的边按逆时针方向运动一周回到A点，所示四个图中，函数y=
的图象大致为（ ）
| ln|x+1| |
| x+1 |
A、 |
B、 |
C、 |
D、 |