题目内容
已知实数a，b满足a＜b，则下列结论正确的是（ ）
A、
| ||||
| B、2a＞2b | ||||
| C、lna＜lnb | ||||
| D、a3＜b3 |
考点：不等式的基本性质
专题：计算题,函数的性质及应用
分析：若a，b同号，可判断A，考虑指数函数的单调性，即可判断B，考虑对数函数，即可判断C，考虑幂函数的单调性，即可判断D．
解答：
解：A中，若a，b同号不成立，故A错；
B中，y=2x递增，故B错；
C中，a，b小于0，则无意义，故C错；
D中x3递增，故D正确．
故选D．
B中，y=2x递增，故B错；
C中，a，b小于0，则无意义，故C错；
D中x3递增，故D正确．
故选D．
点评：本题考查不等式的性质，考查函数的单调性及运用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
设集合M={x|x2-2x-3＜0}，N={x|log2（x-1）≤1}，则M∩N等于（ ）
| A、{x|-1＜x＜3} |
| B、{x|1＜x≤3} |
| C、{x|1＜x＜3} |
| D、{x|-1≤x≤3} |
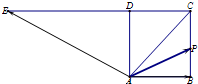如图，四边形ABCD是边长为1的正方形，延长CD至E，使得DE=2CD．动点P从点A出发，沿正方形的边按逆时针方向运动一周回到A点，所示四个图中，函数y=
的图象大致为（ ）
| ln|x+1| |
| x+1 |
A、 |
B、 |
C、 |
D、 |