题目内容
已知数列{an}的前n项和为Sn,且有Sn=
n(an+1),n∈N*,又a2=3
(Ⅰ)写出a1,a3,a4并猜想{an}的通项公式;
(Ⅱ)用数学归纳法证明(1)的猜想结论.
| 1 |
| 2 |
(Ⅰ)写出a1,a3,a4并猜想{an}的通项公式;
(Ⅱ)用数学归纳法证明(1)的猜想结论.
考点:数学归纳法,归纳推理
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)利用递推关系Sn=
n(an+1),n∈N*,及a2=3,可求得a1=1,a3=5,a4=7,于是猜想an=2n-1.
(Ⅱ)利用数学归纳法证明:①当n=1时,易证等式成立,②假设n=k(k≥2)时,利用归纳假设,去推证n=k+1时等式也成立即可.
| 1 |
| 2 |
(Ⅱ)利用数学归纳法证明:①当n=1时,易证等式成立,②假设n=k(k≥2)时,利用归纳假设,去推证n=k+1时等式也成立即可.
解答:
解:(Ⅰ)当n=1时,a1=
(a1+1),解答a1=1,又a2=3,
∴a3=S3-S2=
×3(a3+1)-
×2(a2+1),
解得:a3=5;
同理可得,a4=S4-S3=7;
故猜想:an=2n-1.
(Ⅱ)证明:①当n=1时,a1=1,满足an=2n-1;
②假设n=k(k≥2)时,ak=2k-1,
则n=k+1时,ak+1=Sk+1-Sk=
(k+1)(ak+1+1)-[1+3+5+…+(2k-1)],
∴2ak+1=(k+1)(ak+1+1)-2×
=(k+1)ak+1+k+1-2k2,
∴(k-1)ak+1=2k2-k-1=(k-1)(2k+1),
∵k≥2,
∴ak+1=2k+1=2(k+1)-1,即n=k+1时,等式也成立;
综合①②知,an=2n-1.
| 1 |
| 2 |
∴a3=S3-S2=
| 1 |
| 2 |
| 1 |
| 2 |
解得:a3=5;
同理可得,a4=S4-S3=7;
故猜想:an=2n-1.
(Ⅱ)证明:①当n=1时,a1=1,满足an=2n-1;
②假设n=k(k≥2)时,ak=2k-1,
则n=k+1时,ak+1=Sk+1-Sk=
| 1 |
| 2 |
∴2ak+1=(k+1)(ak+1+1)-2×
| k(1+2k-1) |
| 2 |
∴(k-1)ak+1=2k2-k-1=(k-1)(2k+1),
∵k≥2,
∴ak+1=2k+1=2(k+1)-1,即n=k+1时,等式也成立;
综合①②知,an=2n-1.
点评:本题考查数学归纳法的应用,考查推理.运算能力,猜得an=2n-1是关键,属于中档题.

练习册系列答案
相关题目
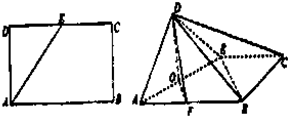 已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△ADE折起,使平面ADE上平面ABCE,点O、F分别是AE、AB的中点.
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△ADE折起,使平面ADE上平面ABCE,点O、F分别是AE、AB的中点.