题目内容
在直三棱柱ABC-A1B1C1中,AB=BC=
,BB1=2,∠ABC=90°,E、F分别为AA1,C1B1的中点,沿棱柱表面,从E到F的最短路径的长为 .
| 2 |
考点:多面体和旋转体表面上的最短距离问题
专题:计算题,空间位置关系与距离
分析:由题意,题中E、F分别在AA1、C1B1上,所以“展开”后的图形中必须有AA1、C1B1,画出图形,分类求出结果,找出最短路径.
解答:
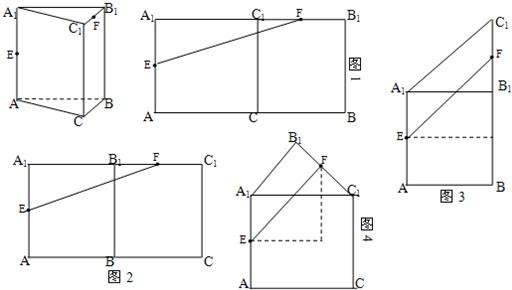
解:题中E、F分别在AA1、C1B1上,所以“展开”后的图形中必须有AA1、C1B1;故“展开”方式有以下四种:
(ⅰ)沿CC1将面ACC1A1和面BCC1B1展开至同一平面,如图1,求得:EF2=
+2
;
(ⅱ)沿BB1将面ABB1A1和面BCC1B1展开至同一平面,如图2,求得:EF2=
+2
;
(ⅲ)沿A1B1将面ABB1A1和面A1B1C1展开至同一平面,如图3,求得:EF2=
+
;
(ⅳ)沿A1C1将面ACC1A1和面A1C1B1展开至同一平面,如图4,求得:EF2=
;
比较可得(ⅳ)情况下,EF的值最小;
故EF的最小值为
.
故答案为:
.
(ⅰ)沿CC1将面ACC1A1和面BCC1B1展开至同一平面,如图1,求得:EF2=
| 11 |
| 2 |
| 2 |
(ⅱ)沿BB1将面ABB1A1和面BCC1B1展开至同一平面,如图2,求得:EF2=
| 7 |
| 2 |
| 2 |
(ⅲ)沿A1B1将面ABB1A1和面A1B1C1展开至同一平面,如图3,求得:EF2=
| 7 |
| 2 |
| 2 |
(ⅳ)沿A1C1将面ACC1A1和面A1C1B1展开至同一平面,如图4,求得:EF2=
| 9 |
| 2 |
比较可得(ⅳ)情况下,EF的值最小;
故EF的最小值为
3
| ||
| 2 |

故答案为:
3
| ||
| 2 |
点评:本题考查把两个平面展开在同一个平面内的方法,利用勾股定理求线段的长度,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目