题目内容
已知函数f(x)=
(a、b为常数,且a≠0)满足f(4)=
,方程f(x)=x有唯一解.
(1)求函数f(x)的解析式;
(2)求f(f(-3))的值.
| x |
| ax+b |
| 4 |
| 3 |
(1)求函数f(x)的解析式;
(2)求f(f(-3))的值.
考点:函数的值
专题:计算题,函数的性质及应用
分析:(1)由题意,求参数a,b,从而确定函数解析式;
(2)代入f(x)=
或f(x)=
求值.
(2)代入f(x)=
| 4 |
| 3 |
| x | ||
|
解答:
解:(1)∵方程f(x)=x有唯一解,又∵a≠0,
∴b=0若b=
,
则又由f(4)=
得,
=
或
=
,
a=
或a=
,
故f(x)=
或f(x)=
,
(2)若f(x)=
,f(f(-3))=
,
若f(x)=
,f(f(-3))=f(
)=f(6)=
=
.
∴b=0若b=
| 1 |
| 2 |
则又由f(4)=
| 4 |
| 3 |
| 4 |
| 4a |
| 4 |
| 3 |
| 4 |
| 4a+1 |
| 4 |
| 3 |
a=
| 3 |
| 4 |
| 1 |
| 2 |
故f(x)=
| 4 |
| 3 |
| x | ||
|
(2)若f(x)=
| 4 |
| 3 |
| 4 |
| 3 |
若f(x)=
| x | ||
|
| -3 | ||
-
|
| 6 |
| 4 |
| 3 |
| 2 |
点评:本题考查了函数的解析式的求法及函数值的求法,属于基础题.

练习册系列答案
相关题目
已知命题p:2x2-x-1<0,那么p成立的一个必要不充分条件是( )
| A、0<x<1 | ||
| B、-1<x<1 | ||
C、-
| ||
D、-
|
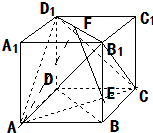 如图所示,在正方形ABCD-A1B1C1D1中,E、F分别是BB1、D1B1的中点.求证:EF⊥平面B1AC.
如图所示,在正方形ABCD-A1B1C1D1中,E、F分别是BB1、D1B1的中点.求证:EF⊥平面B1AC.