题目内容
在区间[0,1]上任意取两个实数a,b,则函数f(x)=
x2+ax-b在区间(-1,1)上有且仅有一个零点的概率为 .
| 1 |
| 2 |
考点:随机事件
专题:概率与统计
分析:关键是要找出函数f(x)=
x2+ax-b在区间(-1,1)上有且仅有一个零点时(a,b)点对应的图形的面积,并将其代入几何概型的计算公式,进行求解.
| 1 |
| 2 |
解答:
解:若函数f(x)=
x2+ax-b在区间(-1,1)上有且仅有一个零点,
①△=0时,即a2+2b=0,因为a>0,b>0,所以无解;
②△≠0时,则f(-1)•f(1)<0,
即(
-a-b)(
+a-b)<0,即a2>(
-b)2,
故a,b满足
,
如下图,
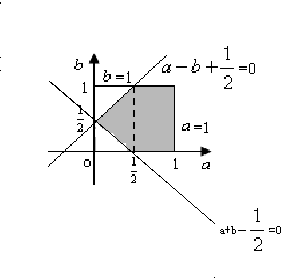
满足条件的(a,b)落在阴影上,
∵S阴影=1-
=
,
∴函数f(x)=
x2+ax-b在区间(-1,1)上有且仅有一个零点的概率为P=
=
=
;
故答案为:
.
| 1 |
| 2 |
①△=0时,即a2+2b=0,因为a>0,b>0,所以无解;
②△≠0时,则f(-1)•f(1)<0,
即(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故a,b满足
|
如下图,

满足条件的(a,b)落在阴影上,
∵S阴影=1-
| 1 |
| 4 |
| 3 |
| 4 |
∴函数f(x)=
| 1 |
| 2 |
| S阴影 |
| S矩形 |
| ||
| 1 |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查了几何概型的概率估算公式的运用;几何概型概率的计算中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
相关题目