题目内容
 如图,在30°的二面角α-l-β的棱上有两点A,B,点C,D分别在α,β内,且AC⊥AB,BD⊥AB,AC=BD=AB=1,则CD的长度为
如图,在30°的二面角α-l-β的棱上有两点A,B,点C,D分别在α,β内,且AC⊥AB,BD⊥AB,AC=BD=AB=1,则CD的长度为考点:二面角的平面角及求法
专题:空间位置关系与距离
分析:
2=(
+
+
)2,由此能求出结果.
| CD |
| CA |
| AB |
| BD |
解答:
解:∵在30°的二面角α-l-β的棱上有两点A,B,
点C,D分别在α,β内,且AC⊥AB,BD⊥AB,AC=BD=AB=1,
∴
2=(
+
+
)2
=1+1+1+2×1×1×cos150°
=3-
,
∴CD的长度为
.
故答案为:
.
点C,D分别在α,β内,且AC⊥AB,BD⊥AB,AC=BD=AB=1,
∴
| CD |
| CA |
| AB |
| BD |
=1+1+1+2×1×1×cos150°
=3-
| 3 |
∴CD的长度为
3-
|
故答案为:
3-
|
点评:本题考查线段长的求法,是基础题,解题时要注意空间向量加法定理的合理运用.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
已知数列{an}满足条件:a1=
,an+1=
(n∈N+),则对n≤20的正整数,an+an+1=
的概率为( )
| 1 |
| 2 |
| 1+an |
| 1-an |
| 1 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
| D、0 |
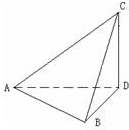 如图,将边长为1m的正△ABC沿高AD折叠成直二面角B-AD-C,则直线AC与直线AB所成角的余弦值是
如图,将边长为1m的正△ABC沿高AD折叠成直二面角B-AD-C,则直线AC与直线AB所成角的余弦值是