题目内容
6.在△ABC中,三个内角A、B、C成等差数列,且cosA=$\frac{2}{3}$,则sinC=( )| A. | $\frac{-2\sqrt{3}+\sqrt{5}}{6}$ | B. | $\frac{2\sqrt{3}+\sqrt{5}}{6}$ | C. | $\frac{2\sqrt{3}-\sqrt{5}}{6}$ | D. | $\frac{-2\sqrt{3}-\sqrt{5}}{6}$ |
分析 直接由等差数列的性质结合三角形内角和定理得B的值,利用同角三角函数基本关系式可求sinA,进而利用两角和的正弦函数公式可求sinC的值.
解答 解:∵∠A、∠B、∠C成等差数列,
∴∠A+∠C=2∠B,
又∠A+∠B+∠C=π,
∴3∠B=π,则∠B=$\frac{π}{3}$.
∵cosA=$\frac{2}{3}$,可得:sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{\sqrt{5}}{3}$,
∴sinC=sin(A+B)=sinAcosB+cosAsinB=$\frac{\sqrt{5}}{3}$×$\frac{1}{2}$+$\frac{2}{3}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{5}+2\sqrt{3}}{6}$.
故选:B.
点评 本题主要考查了等差数列的性质,考查了同角三角函数基本关系式,两角和的正弦函数公式,三角形内角和定理,是基础题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
17.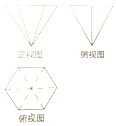 一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的体积是( )
一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的体积是( )
 一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的体积是( )
一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的体积是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $\frac{3}{2}$ |
14.为了得到函数y=1-2sin2(x-$\frac{π}{12}$)的图象,可以将函数y=sin2x的图象( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{π}{3}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
1.101(9)化为十进制数为( )
| A. | 9 | B. | 11 | C. | 82 | D. | 101 |
16.已知集合A={-3,-2,-1,0,1,2},B={x|(x+3)(x-1)<0},则A∩B=( )
| A. | {0,1,2} | B. | {-2,-1,0} | C. | {-3,-2,-1,0,1} | D. | {0,1,2,3} |
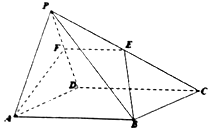 如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E、F分别是棱PC和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E、F分别是棱PC和PD的中点.