题目内容
17．
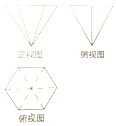一个几何体的三视图如图所示，其中正视图是边长为2的等边三角形，俯视图为正六边形，则该几何体的体积是（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | 2 | D． | $\frac{3}{2}$ |
分析 该几何体是正六棱锥，依据数据求解即可．
解答 解：由三视图可知几何体是正六棱锥，底面边长为1，侧棱长为2，
该几何体的体积：$\frac{1}{3}×\sqrt{3}×6×\frac{1}{2}×\frac{\sqrt{3}}{2}$=$\frac{3}{2}$，
故选D．
点评 本题考点是由三视图求几何体的面积、体积，考查对三视图的理解与应用，主要考查三视图与实物图之间的关系，用三视图中的数据还原出实物图的数据，再根据相关的公式求表面积与体积．
练习册系列答案
相关题目
7．已知集合A={x|y=$\sqrt{x-2}$}，B={x|x2-4＜0}，则A∪B=（ ）
| A． | ∅ | B． | （2，+∞） | C． | （-2，+∞） | D． | [0，2） |
8．在Rt△AOB中，$\overrightarrow{OA}$•$\overrightarrow{OB}$=0，|$\overrightarrow{OA}$|=$\sqrt{5}$，|$\overrightarrow{OB}$|=2$\sqrt{5}$，AB边上的高为OD，D在AB上，点E位于线段OD上，若$\overrightarrow{OE}$•$\overrightarrow{EA}$=$\frac{3}{4}$，则向量$\overrightarrow{EA}$在向量$\overrightarrow{OD}$上的投影为（ ）
| A． | $\frac{1}{2}$或$\frac{3}{2}$ | B． | 1 | C． | 1或$\frac{1}{2}$ | D． | $\frac{3}{2}$ |
2．曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1与曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1的（ ）
| A． | 实轴长相等 | B． | 离心率相等 | C． | 范围相同 | D． | 渐近线相同 |
9．下列命题成立的是（ ）
| A． | 若￢p、￢q均为真命题，则p∨q为真命题 | |
| B． | 命题“若x2+2x＜0，则-2＜x＜0”的逆否命题为“若-2＜x＜0，则x2+2x＜0” | |
| C． | 方程x2=1的一个必要不充分条件是x=1 | |
| D． | 抛掷3枚质地均匀的硬币，事件“至少有两枚硬币正面向上”等价于“至多有一枚硬币反面向上” |
6．在△ABC中，三个内角A、B、C成等差数列，且cosA=$\frac{2}{3}$，则sinC=（ ）
| A． | $\frac{-2\sqrt{3}+\sqrt{5}}{6}$ | B． | $\frac{2\sqrt{3}+\sqrt{5}}{6}$ | C． | $\frac{2\sqrt{3}-\sqrt{5}}{6}$ | D． | $\frac{-2\sqrt{3}-\sqrt{5}}{6}$ |