题目内容
已知四面体有5条棱长为2,一条棱长为1,求它的体积.
考点:棱柱、棱锥、棱台的体积
专题:计算题,作图题,空间位置关系与距离
分析:AB=AC=BD=CD=BC=2,AD=1,取AD的中点E,连结BE,CE,作图;VA-BCD=2VA-BCE,从而求体积.
解答:
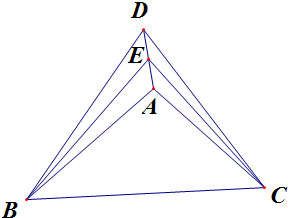 解:如图,AB=AC=BD=CD=BC=2,AD=1,
解:如图,AB=AC=BD=CD=BC=2,AD=1,
取AD的中点E,连结BE,CE,
故可知,AD⊥BE,AD⊥CE,
又∵BE∩CE=E,
∴AD⊥平面BCE,
BE=CE=
=
,
则等腰三角形BEC底边BC上的高为
=
,
则其面积S=
×2×
=
,
VA-BCD=2VA-BCE=2×
×
×
=
.
 解:如图,AB=AC=BD=CD=BC=2,AD=1,
解:如图,AB=AC=BD=CD=BC=2,AD=1,取AD的中点E,连结BE,CE,
故可知,AD⊥BE,AD⊥CE,
又∵BE∩CE=E,
∴AD⊥平面BCE,
BE=CE=
22-
|
| ||
| 2 |
则等腰三角形BEC底边BC上的高为
|
| ||
| 2 |
则其面积S=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
VA-BCD=2VA-BCE=2×
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 6 |
点评:本题考查了学生的作图能力及体积的计算,难在化VA-BCD=2VA-BCE,属于难题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
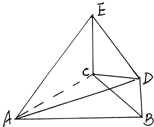 如图,EC⊥平面ABC,EC∥BD,平面ACD⊥平面ECB.
如图,EC⊥平面ABC,EC∥BD,平面ACD⊥平面ECB.