题目内容
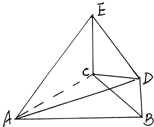 如图,EC⊥平面ABC,EC∥BD,平面ACD⊥平面ECB.
如图,EC⊥平面ABC,EC∥BD,平面ACD⊥平面ECB.(Ⅰ)求证AC⊥BC;
(Ⅱ)若CA=CB=CE=2BD,求二面角D-AE-C的余弦值.
考点:二面角的平面角及求法,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(Ⅰ)由EC⊥平面ABC,AC?平面ABC,EC?平面ABC,得出AC⊥EC,EC⊥BC,∠ACB为A-EC-B的平面角,根据面面垂直可证明.
(Ⅱ)建立坐标系运用向量求解,求解平面DAE的法向量
=(x1,y1,z1),
平面AEC的法向量为
=(x2,y2,z2),运用向量的数量积求解,注意二面角的范围.
(Ⅱ)建立坐标系运用向量求解,求解平面DAE的法向量
| n1 |
平面AEC的法向量为
| n2 |
解答:
(Ⅰ)证明:∵EC∥BD,
∴四边形BDEC为平面图形,
EC⊥平面ABC,AC?平面ABC,EC?平面ABC,
∴AC⊥EC,EC⊥BC,
∴∠ACB为A-EC-B的平面角,
∴∠ACB=90°,
∴AC⊥BC;
(Ⅱ)∵AC,BC,EC两两垂直,
∴分别以CA,CB,CE为x,y,z轴,建立坐标系,
∵CA=CB=CE=2BD,
∴A(2,0,0),C(0,0,0),E(0,0,2),D(0,2,1),
∴
=(-2,0,2),
=(-2,2,1),
=(0,0,2),
设平面DAE的法向量
=(x1,y1,z1),平面AEC的法向量为
=(x2,y2,z2),
∴
,得
=(1,
,1),
,得
=(0,1,0),
∴cos<
,
>=
=
=
∵二面角D-AE-C是锐二面角,
∴二面角D-AE-C的余弦值为:
.
∴四边形BDEC为平面图形,
EC⊥平面ABC,AC?平面ABC,EC?平面ABC,
∴AC⊥EC,EC⊥BC,
∴∠ACB为A-EC-B的平面角,
∴∠ACB=90°,
∴AC⊥BC;
(Ⅱ)∵AC,BC,EC两两垂直,
∴分别以CA,CB,CE为x,y,z轴,建立坐标系,
∵CA=CB=CE=2BD,
∴A(2,0,0),C(0,0,0),E(0,0,2),D(0,2,1),
∴
| AE |
| AD |
| CE |
设平面DAE的法向量
| n1 |
| n2 |
∴
|
| n1 |
| 1 |
| 2 |
|
| n2 |
∴cos<
| n1 |
| n2 |
| ||||
|
|
| ||||
|
| 1 |
| 3 |
∵二面角D-AE-C是锐二面角,
∴二面角D-AE-C的余弦值为:
| 1 |
| 3 |
点评:本题综合考察了空间直线的垂直问题,运用向量求二面角的问题,属于中档题,关键是求解坐标,计算准确.

练习册系列答案
相关题目
如果奇函数f(x)在区间[1,5]上是减函数,且最小值3,那么f(x)在区间[-5,-1]上是( )
| A、增函数且最小值为3 |
| B、增函数最大值为3 |
| C、减函数且最小值为-3 |
| D、减函数且最大值为-3 |
设P是双曲线
-y2=1上一点,F1、F2是双曲线的焦点,若|PF1|等于1,则|PF2|等于( )
| x2 |
| 4 |
| A、5 | B、3 | C、2 | D、1 |
 已知正方体ABCD-A1B1C1D1,E、F分别是CC1、BB1的中点,求证:平面DEB1∥平面ACF.
已知正方体ABCD-A1B1C1D1,E、F分别是CC1、BB1的中点,求证:平面DEB1∥平面ACF.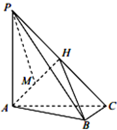 如图,在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,H为PC的中点,M为AH中点,PA=AC=2,BC=1.
如图,在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,H为PC的中点,M为AH中点,PA=AC=2,BC=1.