题目内容
若命题“?x∈R,使x2+(a+1)x+4<0”是假命题,则实数a的取值范围为 .
考点:命题的真假判断与应用
专题:不等式的解法及应用,简易逻辑
分析:写出命题的否定,利用它的否定是真命题进行解答.
解答:
解:命题“?x∈R,使x2+(a+1)x+4<0”的否定是:
“?x∈R,使x2+(a+1)x+4≥0”恒成立;
即△=(a+1)2-16≤0,
解得-5≤a≤3;
∴实数a的取值范围是{a|-5≤a≤3}.
故答案为:{a|-5≤a≤3}.
“?x∈R,使x2+(a+1)x+4≥0”恒成立;
即△=(a+1)2-16≤0,
解得-5≤a≤3;
∴实数a的取值范围是{a|-5≤a≤3}.
故答案为:{a|-5≤a≤3}.
点评:本题考查了不等式的恒成立问题,也考查了命题与命题的否定的应用问题,是基础题.

练习册系列答案
相关题目
已知平面α∥平面β,若两条直线m,n分别在平面α,β内,则m,n的关系不可能是( )
| A、平行 | B、相交 |
| C、异面 | D、平行或异面 |
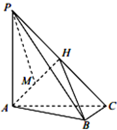 如图,在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,H为PC的中点,M为AH中点,PA=AC=2,BC=1.
如图,在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,H为PC的中点,M为AH中点,PA=AC=2,BC=1.