题目内容
用诱导公式求下列三角函数值.
(1)cos
π;
(2)sin(-
π);
(3)tan(-
)
(1)cos
| 65 |
| 6 |
(2)sin(-
| 31 |
| 4 |
(3)tan(-
| 26π |
| 3 |
考点:运用诱导公式化简求值
专题:计算题,三角函数的求值
分析:运用诱导公式逐一化简即可求值.
解答:
解:(1)cos
π=cos(10π+
)=cos
=-cos
=-
;
(2)sin(-
π)=-sin
=-sin(8π-
)=sin
=
;
(3)tan(-
)=-tan(8π+
)=tan
=
.
| 65 |
| 6 |
| 5π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| ||
| 2 |
(2)sin(-
| 31 |
| 4 |
| 31π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
(3)tan(-
| 26π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| 3 |
点评:本题主要考察了诱导公式化简求值,属于基本知识的考查.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
已知tan(π-α)=
,α∈(
,2π),则cos(α+
)=( )
| 5 |
| 12 |
| 3π |
| 2 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
设P是双曲线
-y2=1上一点,F1、F2是双曲线的焦点,若|PF1|等于1,则|PF2|等于( )
| x2 |
| 4 |
| A、5 | B、3 | C、2 | D、1 |
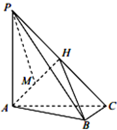 如图,在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,H为PC的中点,M为AH中点,PA=AC=2,BC=1.
如图,在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,H为PC的中点,M为AH中点,PA=AC=2,BC=1.