题目内容
若以连续掷两次骰子分别得到的点数m、n依次作P点的横、纵坐标，则点P满足x2+y2＜16的概率是 ．点P满足|x-2|+|y-2|≤2内的概率是 ．
考点：列举法计算基本事件数及事件发生的概率
专题：计算题,概率与统计
分析：由题意，符合古典概型，计算基本事件共有：6×6=36个；再分别列出满足x2+y2＜16，满足|x-2|+|y-2|≤2的基本事件，从而求概率．
解答：
解：由题意，符合古典概型，
连续掷两次骰子分别得到的点数m、n依次作P点的横、纵坐标，
则其基本事件共有：6×6=36个；
点P满足x2+y2＜16的有（1，2），（1，1），（1，3）；（2，1），（2，2），（2，3）；（3，1），（3，2）；共8个，
故P=
=
；
点P满足|x-2|+|y-2|≤2的有：（1，1），（1，2），（1，3）；（2，1），（2，2），（2，3），（2，4）；
（3，1），（3，2），（3，3）；（4，2）；共有11个，
故P=
；
故答案为：
，
．
连续掷两次骰子分别得到的点数m、n依次作P点的横、纵坐标，
则其基本事件共有：6×6=36个；
点P满足x2+y2＜16的有（1，2），（1，1），（1，3）；（2，1），（2，2），（2，3）；（3，1），（3，2）；共8个，
故P=
| 8 |
| 36 |
| 2 |
| 9 |
点P满足|x-2|+|y-2|≤2的有：（1，1），（1，2），（1，3）；（2，1），（2，2），（2，3），（2，4）；
（3，1），（3，2），（3，3）；（4，2）；共有11个，
故P=
| 11 |
| 36 |
故答案为：
| 2 |
| 9 |
| 11 |
| 36 |
点评：本题考查了概率模型的判断及古典概型概率的求法，属于基础题．
练习册系列答案
相关题目
已知正方体ABCD-A1B1C1D1，E、F分别是CC1、BB1的中点，求证：平面DEB1∥平面ACF．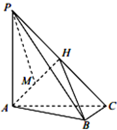
如图，在三棱锥P-ABC中，PA⊥底面ABC，AC⊥BC，H为PC的中点，M为AH中点，PA=AC=2，BC=1．已知平面α∥平面β，若两条直线m，n分别在平面α，β内，则m，n的关系不可能是（ ）
| A、平行 | B、相交 |
| C、异面 | D、平行或异面 |