题目内容
8．已知正方体的表面积为24，则该正方体的体积为（ ）| A． | 8 | B． | 27 | C． | 64 | D． | 125 |
分析 由正方体的表面积为24，求出正方体的棱长，由此能求出正方体的体积．
解答 解：设正方体的棱长为a．
∵正方体的表面积为24，
∴6a2=24，解得a=2，
∴该正方体的体积为V=23=8．
故选：A．
点评 本题考查正方体性质及体积计算等基础知识；考查学生的空间想象能力、推理论证能力及运算求解能力；考查了化归与转化及数形结合的数学思想．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
18．在正四面体ABCD中，E，F分别为棱AD，BC的中点，连接AF，CE，则异面直线AF与CE所成角的余弦值为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{{\sqrt{2}}}{3}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
19．
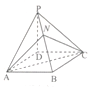如图，四棱锥P-ABCD的底面ABCD为平行四边形，NB=2PN，则三棱锥N-PAC与三棱锥D-PAC的体积之比为（ ）
如图，四棱锥P-ABCD的底面ABCD为平行四边形，NB=2PN，则三棱锥N-PAC与三棱锥D-PAC的体积之比为（ ）| A． | 1：2 | B． | 1：3 | C． | 1：4 | D． | 1：6 |
16．下列命题中的真命题为（ ）
| A． | ?x0∈Z，使得1＜4x0＜3 | B． | ?x0∈Z，使得5x0+1=0 | ||
| C． | ?x∈R，x2-1=0 | D． | ?x∈R，x2+x+2＞0 |
3．
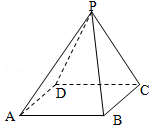如图，在正四棱锥P-ABCD中，AB=2$\sqrt{3}$，侧面积为8$\sqrt{3}$，则它的体积为（ ）
如图，在正四棱锥P-ABCD中，AB=2$\sqrt{3}$，侧面积为8$\sqrt{3}$，则它的体积为（ ）| A． | 4 | B． | 8 | C． | 12π | D． | 16π |