题目内容
11.已知函数f(x)=$\frac{1}{2}$-(x-$\sqrt{e}$)(x-$\frac{1}{2}$)(其中x∈(0,+∞)),g(x)=lnx和函数h(x)=$\left\{\begin{array}{l}{f(x)}&{f(x)≥g(x)}\\{g(x)}&{f(x)<g(x)}\end{array}\right.$,若方程h(x)=kx有四个不同的解,则实数k的取值范围是( )| A. | (0,$\frac{1}{2}$) | B. | (0,$\frac{\sqrt{e}}{2e}$) | C. | ($\frac{\sqrt{e}}{2e}$,$\frac{1}{e}$) | D. | ($\frac{1}{e}$,$\frac{\sqrt{e}}{e}$) |
分析 作出函数图象,求出切线斜率,根据交点个数得出k的范围.
解答 解:作出h(x)的函数图象如图所示: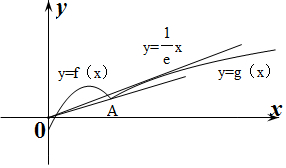
设直线y=kx与曲线g(x)=lnx相切,切点为(x0,y0),
则有$\left\{\begin{array}{l}{{y}_{0}=k{x}_{0}}\\{{y}_{0}=ln{x}_{0}}\\{\frac{1}{{x}_{0}}=k}\end{array}\right.$,解得k=$\frac{1}{e}$.
∵h(x)=kx有四个不同的解,
∴直线y=kx与f(x)有2个交点,y=kx与g(x)有2个交点,
∴k<$\frac{1}{e}$,排除D,
设f(x)与g(x)的交点为A,显然A在第一象限,即kOA>0,
∴k>kOA.排除A,B.
故选C.
点评 本题考查了函数的图象与性质,导数的几何意义,属于中档题.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
16. 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有f(x1+x2)=$\sqrt{3}$,则φ的值为( )
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有f(x1+x2)=$\sqrt{3}$,则φ的值为( )
 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有f(x1+x2)=$\sqrt{3}$,则φ的值为( )
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有f(x1+x2)=$\sqrt{3}$,则φ的值为( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
2.甲、乙两企业生产同一种型号零件,按规定该型号零件的质量指标值落在[45,75)内为优质品,从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如表:
甲企业:
乙企业:
(1)已知甲企业的500件产品质量指标值的样本方差s2=142,该企业生产的零件质量指标值X服从正态分布N(μ,σ2),其中μ近似为质量指标值的样本平均数$\overline{x}$(注:求$\overline{x}$时,同一组数据用该区间的中点值作代表),σ2近似为样本方差s2,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率(精确到0.001)
(2)由以上统计数据完成下面2×2列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”
附注:
参考数据:$\sqrt{142}$≈11.92
参考公式:P(μ-σ<X<μ+σ)=0.6827,P(μ-2σ<X<μ+2σ)=0.9545,P(μ-3σ<X<μ+3σ)=0.9973.
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
甲企业:
| 分组 | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) | [75,85) | [85,95) |
| 频数 | 10 | 40 | 115 | 165 | 120 | 45 | 5 |
| 分组 | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) | [75,85) | [85,95) |
| 频数 | 5 | 60 | 110 | 160 | 90 | 70 | 5 |
(2)由以上统计数据完成下面2×2列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | |||
| 非优质品 | |||
| 合计 |
参考数据:$\sqrt{142}$≈11.92
参考公式:P(μ-σ<X<μ+σ)=0.6827,P(μ-2σ<X<μ+2σ)=0.9545,P(μ-3σ<X<μ+3σ)=0.9973.
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
19. 一货轮航行至M处,测得灯塔S在货轮的北偏西15°,与灯塔相距80海里,随后货轮沿北偏东45°的方向航行了50海里到达N处,则此时货轮与灯塔S之间的距离为( )
一货轮航行至M处,测得灯塔S在货轮的北偏西15°,与灯塔相距80海里,随后货轮沿北偏东45°的方向航行了50海里到达N处,则此时货轮与灯塔S之间的距离为( )
 一货轮航行至M处,测得灯塔S在货轮的北偏西15°,与灯塔相距80海里,随后货轮沿北偏东45°的方向航行了50海里到达N处,则此时货轮与灯塔S之间的距离为( )
一货轮航行至M处,测得灯塔S在货轮的北偏西15°,与灯塔相距80海里,随后货轮沿北偏东45°的方向航行了50海里到达N处,则此时货轮与灯塔S之间的距离为( )| A. | 70海里 | B. | 10 129海里 | ||
| C. | 10 79海里 | D. | 10 89-40 3海里 |
16.已知函数f(x)=sin2$\frac{ωx}{2}$+$\frac{1}{2}$sinωx-$\frac{1}{2}$(ω>0),x∈R.若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
| A. | (0,$\frac{1}{8}$] | B. | (0,$\frac{1}{4}$]∪[$\frac{5}{8}$,1) | C. | (0,$\frac{5}{8}$] | D. | (0,$\frac{1}{8}$]∪($\frac{1}{4}$,$\frac{5}{8}$] |
3.已知等差数列{an}的前n项和为Sn,公差为1,若S6=3S3,则a9=( )
| A. | 11 | B. | $\frac{19}{2}$ | C. | 9 | D. | 10 |
11.集合A中的元素个数用符号card(A)表示,设A={x|(lnx)2+mx2lnx>0},N为自然数集,若card(A∩N)=3,则实数m的取值范围是( )
| A. | (-$\frac{ln2}{4}$,-$\frac{ln2}{8}$] | B. | (-$\frac{ln2}{8}$,-$\frac{ln5}{30}$] | C. | (-$\frac{ln2}{8}$,-$\frac{ln5}{25}$] | D. | (-$\frac{ln3}{9}$,-$\frac{ln2}{8}$] |