题目内容
5.已知某程序框图如图所示,则执行该程序后输出的结果是-1.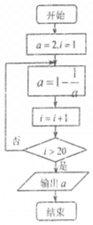
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算变量a的值并输出.
解答 解:程序运行过程中,各变量的值如下表示:
a i 是否继续循环
循环前 2 1
第一圈 a=$\frac{1}{2}$,i=2 是循环
第二圈 a=-1,i=3 是循环
第三圈 a=2,i=4 是循环
第四圈 a=$\frac{1}{2}$,5 是循环
…
观察规律可得a的取值周期为3,由于20=3×6+2,可得
第19圈 a=$\frac{1}{2}$,i=20 是循环
第20圈 a=-1,i=21 否循环
输出a的值为-1.
故答案为:-1.
点评 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中既要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
16.在拍毕业照时,六个同学排成一排照相,要求其中一对好友甲和乙相邻,且同学丙不能和甲相邻的概率为( )
| A. | $\frac{1}{15}$ | B. | $\frac{2}{15}$ | C. | $\frac{4}{15}$ | D. | $\frac{1}{5}$ |
10.已知向量$\overrightarrow{a}$=(x-1,2),$\overrightarrow{b}$=(y,-4),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则4x+2y的最小值为( )
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
17.已知O是坐标原点,双曲线${x^2}-\frac{y^2}{n^2}=1({n>0})$的两条渐近线分别为l1,l2,右焦点为F,以OF为直径的圆交l1于异于原点O的点A,若点B在l2上,且$\frac{1}{2}\overrightarrow{BA}=\overrightarrow{AF}$,则双曲线的方程为( )
| A. | ${x^2}-\frac{y^2}{3}=1$ | B. | ${x^2}-\frac{y^2}{2}=1$ | C. | ${x^2}-\frac{y^2}{5}=1$ | D. | ${x^2}-\frac{y^2}{6}=1$ |
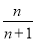 ,则
,则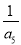 等于( )
等于( )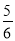 B.
B.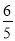 C.
C.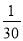 D.30
D.30