已知$\overrightarrow{a}$=(1.2).$\overrightarrow{a}$-2$\overrightarrow{b}$=.则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值为$\frac{4}{5}$．题目和参考答案——青夏教育精英家教网—

题目内容

13．已知$\overrightarrow{a}$=（1，2），$\overrightarrow{a}$-2$\overrightarrow{b}$=（-7，-2），则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值为$\frac{4}{5}$．

分析利用两个向量的数量积的定义，两个向量的数量积公式，求得$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值．

解答解：设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ，∵已知$\overrightarrow{a}$=（1，2），$\overrightarrow{a}$-2$\overrightarrow{b}$=（-7，-2），∴$\overrightarrow{b}$=（4，2），
∴$\overrightarrow{a}•\overrightarrow{b}$=1×4+2×2=8，再根据$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cosθ=$\sqrt{5}$•$\sqrt{20}$•cosθ，
可得$\sqrt{5}$•$\sqrt{20}$•cosθ=8，求得cosθ=$\frac{4}{5}$，
故答案为：$\frac{4}{5}$．

点评本题主要考查两个向量的数量积的定义，两个向量的数量积公式，属于基础题．

练习册系列答案

	A．	t=-$\frac{\sqrt{3}}{2}$，m的最小值为$\frac{π}{6}$		B．	t=-$\frac{\sqrt{3}}{2}$，m的最小值为$\frac{π}{12}$
	C．	t=-$\frac{1}{2}$，m的最小值为$\frac{π}{12}$		D．	t=-$\frac{1}{2}$，m的最小值为$\frac{π}{6}$

4．学生在野营活动中，用直杆搭建一个支架进行野炊，如图1所示，已知PA=PB=PC=140cm，点C到A、B两点的距离相等，E、F、G、H分别是PA、PB、PC、EF的中点，直杆GH与底面ABC的距离为50cm．

（1）在图2中画出相应于图1的空间图形；三棱锥P-ABC及相关线段EF、GH；
（2）求PC与底面ABC所成角的大小（结果用反三角形式表示）；
（3）判断PC与EF是否互相垂直，并说明理由．

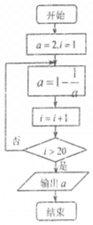
1．如果执行如图所示的程序框图，则输出的结果是（　　）

8．已知函数f（x）=ae^x+（2-e）x（a为实数，e为自然对数的底数），曲线y=f（x）在x=0处的切线与直线（3-e）x-y+10=0平行．
（1）求实数a的值，并判断函数f（x）在区间[0，+∞）内的零点个数；
（2）证明：当x＞0时，f（x）-1＞xln（x+1）．

18．已知曲线C的参数方程为$\left\{\begin{array}{l}{x=2+3cosα}\\{y=1+3sinα}\end{array}\right.$（α为参数），直线l的参数方程为$\left\{\begin{array}{l}{x=t}\\{y=-t}\end{array}\right.$（t为参数），以原点为极点，x轴非负半轴为极轴建立坐标系．
（1）求曲线C和直线l的极坐标方程；
（2）求曲线C和直线l的交点的极坐标．

5．已知某程序框图如图所示，则执行该程序后输出的结果是-1．

2．已知各项均为正数的等比数列{a_n}，前n项和为S_n，${a_2}{a_8}={a_m}^2=1024$且a₁=2，则S_m=62．

3．若（a²+2b³）ⁿ的展开式中有一项为ma⁴b¹²，则m=240．

试题分类