题目内容
10.已知向量$\overrightarrow{a}$=(x-1,2),$\overrightarrow{b}$=(y,-4),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则4x+2y的最小值为( )| A. | 4 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
分析 利用向量共线定理及$\overrightarrow{a}$∥$\overrightarrow{b}$,可得x,y的关系式,再利用基本不等式即可得出
解答 解:∵$\overrightarrow{a}$=(x-1,2),$\overrightarrow{b}$=(y,-4),$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴-4(x-1)=2y,
∴2x+y=2,
∴2=2x+y,
∴4x+2y≥2$\sqrt{{2}^{2x}•{2}^{y}}$=2$\sqrt{{2}^{2x+y}}$=2$\sqrt{{2}^{2}}$=4,当且仅当x=$\frac{1}{2}$,y=1时取等号,
∴则4x+2y的最小值为4,
故选:A.
点评 本题考查了向量共线定理、基本不等式的性质等基础知识与基本方法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
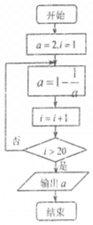
1.如果执行如图所示的程序框图,则输出的结果是( )


| A. | -4 | B. | -3 | C. | 2 | D. | 0 |
15.已知实数x,y满足$\left\{\begin{array}{l}y≥1\\ 2x≥1+y\\ x≤m-y\end{array}\right.$,如果目标函数$z=\frac{3}{2}x-y$的最大值为3,则m的值为( )
| A. | 3 | B. | $\frac{11}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{8}{3}$ |
19.已知复数z满足(z-5)(1-i)=1+i,则复数z的共轭复数为( )
| A. | 5+i | B. | 5-i | C. | -5+i | D. | -5-i |
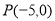 ,点
,点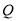 是圆
是圆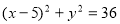 上的点,
上的点,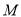 是线段
是线段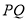 的中点.
的中点.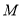 的轨迹
的轨迹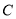 的方程;
的方程; 的直线
的直线 和轨迹
和轨迹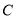 有两个交点
有两个交点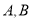 (
(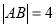 ,求直线
,求直线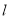 的方程.
的方程.