题目内容
6．若直线2ax-by+2=0（a＞0，b＞0），经过圆x2+y2+2x-4y+1=0的圆心，则$\frac{1}{a}+\frac{1}{b}$的最小值是（ ）| A． | $\frac{1}{2}$ | B． | 2 | C． | $\frac{1}{4}$ | D． | 4 |
分析 求出圆的圆心坐标，代入直线方程，得到ab关系式，然后通过”1“的代换利用基本不等式求解即可．
解答 解：x2+y2+2x-4y+1=0的圆心（-1，2），
所以直线2ax-by+2=0（a＞0，b＞0）经过圆心，可得：a+b=1，
$\frac{1}{a}+\frac{1}{b}$=（$\frac{1}{a}+\frac{1}{b}$）（a+b）=2+$\frac{b}{a}$+$\frac{a}{b}$≥4，当且仅当a=b=$\frac{1}{2}$，
所以$\frac{1}{a}+\frac{1}{b}$的最小值是：4．
故选：D．
点评 本题考查直线与圆的位置关系的应用，基本不等式求解函数的最值，考查转化思想以及计算能力．
练习册系列答案
相关题目
14．已知函数f（x）=sinx-bcosx（其中b为实数）的图象关于直线x=-$\frac{π}{6}$对称，且?x1，x2∈R，且x1≠x2，f（x1）f（x2）≤4恒成立，则下列结论正确的是（ ）
| A． | 函数f（x）的图象向左平移$\frac{π}{3}$个单位得到的函数是偶函数 | |
| B． | 不等式f（x1）f（x2）≤4取到等号时|x1-x2|的最小值为2π | |
| C． | 函数f（x）的图象的一个对称中心为（$\frac{2}{3}$π，0） | |
| D． | 函数f（x）在区间[$\frac{π}{6}$，π]上单调递增 |
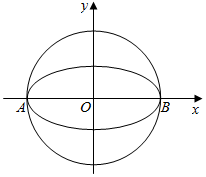如图，椭圆W：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，其左顶点A在圆O：x2+y2=16上．
11．设a是实数，且$\frac{2a}{1+i}$+1+i是实数，则a=（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | -1 |