题目内容
若关于x的不等式x2+ax-2>0在区间[1,4]上有解,则实数a的取值范围为( )
A、(-
| ||
B、[-
| ||
| C、(1,+∞) | ||
D、(-
|
考点:一元二次不等式的解法
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:关于x的不等式x2+ax-2>0在区间[1,4]上有解?a>(
-x)min,x∈[1,4].利用函数的单调性即可得出.
| 2 |
| x |
解答:
解:∵关于x的不等式x2+ax-2>0在区间[1,4]上有解,
∴a>
-x,x∈[1,4],
?a>(
-x)min,x∈[1,4],
∵函数f(x)=
-x在x∈[1,4]单调递减,
∴当x=4时,函数f(x)取得最小值-
,
∴实数a的取值范围为(-
,+∞).
故选A.
∴a>
| 2 |
| x |
?a>(
| 2 |
| x |
∵函数f(x)=
| 2 |
| x |
∴当x=4时,函数f(x)取得最小值-
| 7 |
| 2 |
∴实数a的取值范围为(-
| 7 |
| 2 |
故选A.
点评:本题考查了函数的单调性、分离参数法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
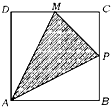 如图,点P在边长为1的正方形的边上运动,设M是CD的中点,则当P沿着路径A-B-C-M运动时,点P经过的路程x与△APM的面积y的函数关系为y=f(x),则y=f(x)的图象是
如图,点P在边长为1的正方形的边上运动,设M是CD的中点,则当P沿着路径A-B-C-M运动时,点P经过的路程x与△APM的面积y的函数关系为y=f(x),则y=f(x)的图象是( )
A、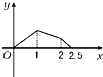 |
B、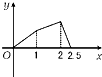 |
C、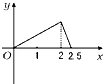 |
D、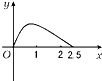 |
已知向量
=(-1,2),
=(m,-1),
=(3,-2),若(
-
)⊥
,则m的值是( )
| a |
| b |
| c |
| a |
| b |
| c |
A、
| ||
B、
| ||
| C、3 | ||
| D、-3 |
已知棱长为1的正方体的俯视图是边长为1正方形,则其主视图的面积不可能是( )
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
不等式的(x-2)(2x-3)<0解集是( )
A、(-∞,
| ||
| B、R | ||
C、(
| ||
| D、φ |
下列函数中,既是偶函数又在(0,π)上单调递增的是( )
| A、y=sinx | ||
| B、y=tan|x| | ||
C、y=sin(x-
| ||
| D、y=cos(-x) |
已知X=logmn,则mn>1是X>1的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |