题目内容
15.小李参加一种红包接龙游戏:他在红包里塞了12元,然后发给朋友A,如果A猜中,A将获得红包里的所有金额;如果A未猜中,A将当前的红包转发给朋友B,如果B猜中,A、B平分红包里的金额;如果B未猜中,B将当前的红包转发给朋友C,如果C猜中,A、B和C平分红包里的金额;如果C未猜中,红包里的钱将退回小李的账户,设A、B、C猜中的概率分别为$\frac{1}{3}$,$\frac{1}{2}$,$\frac{1}{3}$,且A、B、C是否猜中互不影响.(1)求A恰好获得4元的概率;
(2)设A获得的金额为X元,求X的分布列;
(3)设B获得的金额为Y元,C获得的金额为Z元,判断A所获得的金额的期望能否超过Y的期望与Z的期望之和.
分析 (1)由相互独立事件概率乘法公式能求出A恰好获得4元的概率.
(2)X的可能取值为0,4,6,12,分别求出相应的概率,由此能求出X的分布列.
(3)Y的可能取值为0,4,6;Z的可能取值为0,4.分别求出相应的概率,由此能求出A所获得的金额的期望能超过Y的期望与Z的期望之和.
解答 解:(1)A恰好获得4元的概率为$\frac{2}{3}×\frac{1}{2}×\frac{1}{3}=\frac{1}{9}$…(2分)
(2)X的可能取值为0,4,6,12,
$P({X=4})=\frac{1}{9},P({X=0})=\frac{2}{3}×\frac{1}{2}×\frac{2}{3}=\frac{2}{9}$,
$P({X=6})=\frac{2}{3}×\frac{1}{2}=\frac{1}{3},P({X=12})=\frac{1}{3}$,…(5分)
所以X的分布列为:
| X | 0 | 4 | 6 | 12 |
| P | $\frac{2}{9}$ | $\frac{1}{9}$ | $\frac{1}{3}$ | $\frac{1}{3}$ |
(3)Y的可能取值为0,4,6;Z的可能取值为0,4.
因为$P({Y=0})=\frac{1}{3}+\frac{2}{3}×\frac{1}{2}×\frac{2}{3}=\frac{5}{9},P({Y=4})=\frac{2}{3}×\frac{1}{2}×\frac{1}{3}=\frac{1}{9},P({Y=6})=\frac{2}{3}×\frac{1}{2}=\frac{1}{3}$,…(8分)
$P({Z=0})=\frac{1}{3}+\frac{2}{3}×\frac{1}{2}+\frac{2}{3}×\frac{1}{2}×\frac{2}{3}=\frac{8}{9},P({Z=4})=\frac{2}{3}×\frac{1}{2}×\frac{1}{3}=\frac{1}{9}$,…(9分)
所以$EY=0×\frac{5}{9}+4×\frac{1}{9}+6×\frac{1}{3}=\frac{22}{9},EZ=0×\frac{8}{9}+4×\frac{1}{9}=\frac{4}{9}$,
所以$EY+EZ=\frac{26}{9}$,
又$EX=0×\frac{2}{9}+4×\frac{1}{9}+6×\frac{1}{3}+12×\frac{1}{3}=\frac{58}{9}$,…(11分)
由于EX>EY+EZ,所以A所获得的金额的期望能超过Y的期望与Z的期望之和.…(12分)
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法及应用,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
16.双曲线$\frac{{x}^{2}}{5}-\frac{{y}^{2}}{2}$=1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{9}$=1(a>0)有相同的焦点,则a的值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{10}$ | C. | 4 | D. | $\sqrt{34}$ |
10.等比数列{an}的第5项恰好等于前5项之和,那么该数列的公比q=( )
| A. | -1 | B. | 1 | C. | 1或-1 | D. | 2 |
7.已知$\frac{sinα-cosα}{sinα+cosα}$=3,则tan2α等于( )
| A. | 2 | B. | $\frac{4}{3}$ | C. | $-\frac{3}{2}$ | D. | 4 |
4.若$\overline z$=$\frac{i}{1+i}$,则z•$\overline z$=( )
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{1}{2}$ |
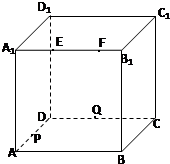 如图,正方体ABCD一A1B1C1D1的棱长为2,动点E,F在棱A1B1上,且EF=1,动点Q在棱CD上,P是棱AD中点,R是棱DDl的中点,则以下结论:
如图,正方体ABCD一A1B1C1D1的棱长为2,动点E,F在棱A1B1上,且EF=1,动点Q在棱CD上,P是棱AD中点,R是棱DDl的中点,则以下结论: