题目内容
14.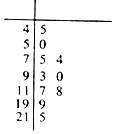 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如下.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如下.(1)利用该样本估计该地本月空气质量优良(AQI≤100)的天数;(按这个月总共30天计算)
(2)若从样本中的空气质量不佳(AQI>100)的这些天,随机地抽取两天深入分析各种污染指标,求这该两天的空气质量等级恰好不同的概率.
分析 (1)利用茎叶图性质和等可能事件概率计算公式能求出该样本中空气质量优良的频率,从而能估计该月空气质量优良的天数.
(2)该样本中空气质量不佳共4天,利用对立事件概率计算公式能求出该两天的空气质量等级恰好不同的概率.
解答 解:(1)从茎叶图中可发现该样本中空气质量优的天数为2,
空气质量良的天数为4,
故该样本中空气质量优良的频率为$\frac{6}{10}=\frac{3}{5}$,
从而估计该月空气质量优良的天数为$30×\frac{3}{5}=18$
(2)该样本中空气质量不佳共4天,
所以该两天的空气质量等级恰好不同的概率为$1-\frac{1}{C_4^2}=\frac{5}{6}$.
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

练习册系列答案
相关题目
2.若数列{an}满足an+12-an2=d(d为正常数,n∈N*),则称{an}为“等方差数列”.甲:数列{an}是等方差数列;乙:数列{an}是等差数列,则( )
| A. | 甲是乙的充分条件但不是必要条件 | |
| B. | 甲是乙的必要条件但不是充分条件 | |
| C. | 甲是乙的充要条件 | |
| D. | 甲既不是乙的充分条件也不是乙的必要条件 |
9.已知命题p:?x0∈R,使2${\;}^{{x}_{0}}$+2${\;}^{-{x}_{0}}$=1;命题q:?x∈R,都有lg(x2+2x+3)>0.下列结论中正确的是( )
| A. | 命题“¬p∧q”是真命题 | B. | 命题“p∧¬q”是真命题 | ||
| C. | 命题“p∧q”是真命题 | D. | 命题“¬p∨¬q”是假命题 |
19.连续两次抛掷一枚骰子,记录向上的点数,则向上的点数之差的绝对值为2的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |
4.若关于x的方程2sin(2x+$\frac{π}{6}$)=m在[0,$\frac{π}{2}$]上有两个不等实根,则m的取值范围是( )
| A. | (1,$\sqrt{3}$) | B. | [0,2] | C. | [1,2) | D. | [1,$\sqrt{3}$] |