题目内容
4.若关于x的方程2sin(2x+$\frac{π}{6}$)=m在[0,$\frac{π}{2}$]上有两个不等实根,则m的取值范围是( )| A. | (1,$\sqrt{3}$) | B. | [0,2] | C. | [1,2) | D. | [1,$\sqrt{3}$] |
分析 把方程2sin(2x+$\frac{π}{6}$)=m化为sin(2x+$\frac{π}{6}$)=$\frac{m}{2}$,画出函数f(x)=sin(2x+$\frac{π}{6}$)在x∈[0,$\frac{π}{2}$]上的图象,结合图象求出方程有两个不等实根时m的取值范围.
解答 解:方程2sin(2x+$\frac{π}{6}$)=m可化为
sin(2x+$\frac{π}{6}$)=$\frac{m}{2}$,
当x∈[0,$\frac{π}{2}$]时,2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
画出函数y=f(x)=sin(2x+$\frac{π}{6}$)在x∈[0,$\frac{π}{2}$]上的图象如图所示;
根据方程2sin(2x+$\frac{π}{6}$)=m在[0,$\frac{π}{2}$]上有两个不等实根,
得$\frac{1}{2}$≤$\frac{m}{2}$<1
1≤m<2
∴m的取值范围是[1,2).
故选:C.
点评 本题主要考查方程根的存在性以及个数判断以及正弦函数的图象应用问题,体现了转化、数形结合的数学思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知集合A={x|x2-2x-3<0},B={x|-2<x<2},则A∩B=( )
| A. | {x|-2<x<2} | B. | {x|-2<x<3} | C. | {x|-1<x<3} | D. | {x|-1<x<2} |
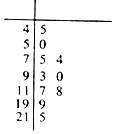 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如下.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如下.