题目内容
3.若函数$f(x)=\sqrt{a{x^2}+bx+c}$(a,b,c∈R)的定义域和值域分别为集合A,B,且集合{(x,y)|x∈A,y∈B}表示的平面区域是边长为1的正方形,则b+c的最大值为5.分析 求出集合A,B,因为{(x,y)|x∈A,y∈B}表示的平面区域是边长为1的正方形,所以$\frac{{\sqrt{{b^2}-4ac}}}{-a}=\sqrt{\frac{{4ac-{b^2}}}{4a}}=1$,可得a=-4,b2+16c=16,$c=1-\frac{b^2}{16}$,即可求出b+c的最大值.
解答 解:由题可知,a<0,b2-4ac>0,则$A=[{\frac{{-b+\sqrt{{b^2}-4ac}}}{2a},\;\;\frac{{-b-\sqrt{{b^2}-4ac}}}{2a}}]$,$B=[{0,\;\;\sqrt{\frac{{4ac-{b^2}}}{4a}}}]$,
因为{(x,y)|x∈A,y∈B}表示的平面区域是边长为1的正方形,所以$\frac{{\sqrt{{b^2}-4ac}}}{-a}=\sqrt{\frac{{4ac-{b^2}}}{4a}}=1$,
可得a=-4,b2+16c=16,$c=1-\frac{b^2}{16}$,所以$b+c=-\frac{b^2}{16}+b+1=-\frac{1}{16}{(b-8)^2}+5$,当b=8时有最大值5.
故答案为5.
点评 本题考查函数的定义域、值域的求法,考查配方法的运用,属于中档题.

练习册系列答案
相关题目
2.已知F1,F2是双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点M在E上,MF1与x轴垂直,sin∠MF2F1=$\frac{1}{3}$,则E的离心率为( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
18.某四棱锥的三视图如图所示,该四棱锥外接球的表面积是( )
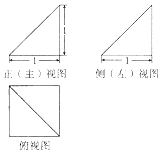

| A. | 4π | B. | 3π | C. | 12π | D. | 8π |
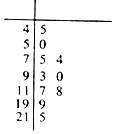 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如下.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如下.