题目内容
5.已知f(x)=2x-2-x,a=($\frac{7}{9}$)${\;}^{-\frac{1}{4}}$,b=($\frac{9}{7}$)${\;}^{\frac{1}{5}}$,c=log2$\frac{7}{9}$,则f(a),f(b),f(c)的大小顺序为( )| A. | f(b)<f(a)<f(c) | B. | f(c)<f(b)<f(a) | C. | f(c)<f(a)<f(b) | D. | f(b)<f(c)<f(a) |
分析 判断出函数f(x)的单调性,求出a,b,c的大小,从而判断出函数值的大小即可.
解答 解:f(x)=2x-2-x在R递增,
而a=($\frac{7}{9}$)${\;}^{-\frac{1}{4}}$>1,0<b=($\frac{9}{7}$)${\;}^{\frac{1}{5}}$<1,c=log2$\frac{7}{9}$<0,
故a>b>c,
则f(a)>f(b)>f(c),
故选:C.
点评 本题考查了函数的单调性问题,考查函数值的大小比较,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知函数f(x)=lnx,g(x)=(2m+3)x+n,若对任意的x∈(0,+∞),总有f(x)≤g(x)恒成立,记(2m+3)n的最小值为f(m,n),则f(m,n)最大值为( )
| A. | 1 | B. | $\frac{1}{e}$ | C. | $\frac{1}{e^2}$ | D. | $\frac{1}{{\sqrt{e}}}$ |
14.已知在△ABC中,内角A,B,C所对的边分别是a,b,c,若sin(B-A)+sin(B+A)=3sin2A,且c=$\sqrt{7}$,C=$\frac{π}{3}$,则△ABC的面积是( )
| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{7\sqrt{3}}{6}$ | C. | $\frac{\sqrt{21}}{3}$ | D. | $\frac{3\sqrt{3}}{4}$或$\frac{7\sqrt{3}}{6}$ |
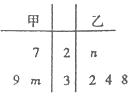 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同.
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同.