题目内容
已知tan(α-π)=
,且α∈(
,
),则sin(α+
)=( )
| 3 |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:由已知tan(α-π)=
得到tanα=
,化为弦函数后与sin2α+cos2α=1联立求得cosα的值,结合α得范围得答案.
| 3 |
| 4 |
| 3 |
| 4 |
解答:
解:由tan(α-π)=
,得tanα=
,
即
=
①
又sin2α+cos2α=1 ②
联立①②解得cosα=±
.
又α∈(
,
),
∴cosα=-
.
∴sin(α+
)=cosα=-
.
故选:B.
| 3 |
| 4 |
| 3 |
| 4 |
即
| sinα |
| cosα |
| 3 |
| 4 |
又sin2α+cos2α=1 ②
联立①②解得cosα=±
| 4 |
| 5 |
又α∈(
| π |
| 2 |
| 3π |
| 2 |
∴cosα=-
| 4 |
| 5 |
∴sin(α+
| π |
| 2 |
| 4 |
| 5 |
故选:B.
点评:本题考查了运用诱导公式化简求值,考查了同角三角函数的基本关系式,是基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
已知函数f(x)=log3x,则f(27)=( )
| A、3 | B、9 | C、27 | D、81 |
下列曲线的所有切线构成的集合中,存在无数对互相垂直的切线的曲线是( )
| A、f(x)=cosx |
| B、f(x)=ex |
| C、f(x)=x3 |
| D、f(x)=lnx |
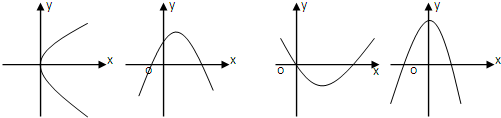
在下面的四个图象中,其中一个图象是函f(x)=
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( )
| 1 |
| 3 |

A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知命题p:?x∈R,x+
≥2;命题q:?x∈R,x2-x+1<0.则下列结论中正确的是( )
| 1 |
| x |
| A、p∧q为真命题 |
| B、p∧¬q为真命题 |
| C、¬p∧q为真命题 |
| D、¬p∧¬q为真命题 |
下列程序框图中是执行框的图形符号的是( )
A、 |
B、 |
C、 |
D、 |
已知函数f(x)=cos(2x+φ)(|φ|<
)的图象向左平移
个单位后的一条对称轴为x=
,则φ的取值为( )
| π |
| 2 |
| π |
| 6 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|