题目内容
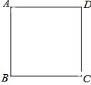 如图,在正方形ABCD中,求正方形内一点到A,B,D的距离和最短.
如图,在正方形ABCD中,求正方形内一点到A,B,D的距离和最短.考点:两点间的距离公式,函数的最值及其几何意义
专题:计算题,解三角形
分析:以D为旋转中心,将△APD旋转60°得到△A'P'D,连P'P,PB,易得△PP'D为等边三角形,即PP'=PD,则AP+PB+PD=A'P'+P'P+PB,当AP+PB+PD取最小值时,折线A'P'PB成为线段,由余弦定理求得最小值,以及最小值时,∠APD=120°,∠PAD=45°,∠ADP=15°,即可确定P点.
解答:
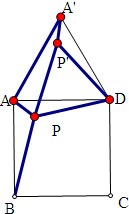 解:以D为旋转中心,将△APD旋转60°得到△A'P'D,连P'P,PB,如图,
解:以D为旋转中心,将△APD旋转60°得到△A'P'D,连P'P,PB,如图,
∴PD=P'D,∠PDP'=60°,
∴△PP'D为等边三角形,
∴PP'=PD,
∴AP+PB+PD=A'P'+P'P+PB,
当AP+PB+PD取最小值时,折线A'P'PB成为线段,
∴∠A'AB=150°,设正方形边长为a,则由余弦定理可得,
最小值为
=
a.
易得取最小值时,∠APD=120°,∠PAD=45°,∠ADP=15°,
即可得到所求P点.
 解:以D为旋转中心,将△APD旋转60°得到△A'P'D,连P'P,PB,如图,
解:以D为旋转中心,将△APD旋转60°得到△A'P'D,连P'P,PB,如图,∴PD=P'D,∠PDP'=60°,
∴△PP'D为等边三角形,
∴PP'=PD,
∴AP+PB+PD=A'P'+P'P+PB,
当AP+PB+PD取最小值时,折线A'P'PB成为线段,
∴∠A'AB=150°,设正方形边长为a,则由余弦定理可得,
最小值为
a2+a2-2a2•(-
|
2+
|
易得取最小值时,∠APD=120°,∠PAD=45°,∠ADP=15°,
即可得到所求P点.
点评:本题考查了旋转的性质:旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角.也考查了等边三角形的性质、余弦定理以及两点之间线段最短.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
已知定义在R上的奇函数f(x)满足f(x+1)=f(x),当0<x<
时,f(x)=4x,则f(-
)=( )
| 1 |
| 2 |
| 5 |
| 4 |
A、-
| ||||
B、-
| ||||
| C、-1 | ||||
D、
|
在某一试验中事件A出现的概率为p,则在n次试验中
出现k次的概率为( )
. |
| A |
| A、1-pk | ||
| B、(1-p)kpn-k | ||
| C、1-(1-p)k | ||
D、
|
△ABC中,a=8,A=45°,C=75°则b=( )
A、4
| ||
B、4
| ||
C、4
| ||
D、4(
|
已知集合M={1,2,3},N={x∈Z|1<x<4},则( )
| A、M⊆N |
| B、N=M |
| C、M∩N={2,3} |
| D、M∪N={1,4} |