题目内容
如图，四棱锥S一ABCD中，已知AD∥BC，∠ADC=90°，∠BAD=135°，AD=DC=| 2 |
（I）求证：AC⊥SD；
（Ⅱ）求二面角A-SB-C的余弦值．
考点：二面角的平面角及求法
专题：空间位置关系与距离,空间角
分析：（Ⅰ）取AC的中点O，连接OD，由已知得AC⊥平面SOD，由此能证明AC⊥SD．
（Ⅱ）由题意知OA=OC=OD，SA=SC=SD，从而SO⊥平面ABCD，连接BO，则∠SBO为直线SB与平面ABCD所成的角，由此能求出二面角A-SB-C的余弦值．
（Ⅱ）由题意知OA=OC=OD，SA=SC=SD，从而SO⊥平面ABCD，连接BO，则∠SBO为直线SB与平面ABCD所成的角，由此能求出二面角A-SB-C的余弦值．
解答：
（Ⅰ）证明：如图，取AC的中点O，连接OD，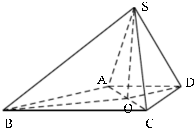
∵AD=DC，∴AC⊥OD，
又∵SA=SC，∴AC⊥OS，
由OD∩OS=O，得AC⊥平面SOD，
∵SD?平面SOD，∴AC⊥SD．
（Ⅱ）解：由题意知OA=OC=OD，
∵SA=SC=SD，
∴O是点S在平面ABCD上的射影，
故SO⊥平面ABCD，
连接BO，则∠SBO为直线SB与平面ABCD所成的角，
由题意知∠BAC=90°，∠ACB=45°，
∴△ABC为等腰直角三角形，
且AB=AC=2，∴BO=
，
在Rt△SBO中，SB=
=2
，
∴cos∠SBO=
=
，
∴二面角A-SB-C的余弦值为
．
∵AD=DC，∴AC⊥OD，
又∵SA=SC，∴AC⊥OS，
由OD∩OS=O，得AC⊥平面SOD，
∵SD?平面SOD，∴AC⊥SD．
（Ⅱ）解：由题意知OA=OC=OD，
∵SA=SC=SD，
∴O是点S在平面ABCD上的射影，
故SO⊥平面ABCD，
连接BO，则∠SBO为直线SB与平面ABCD所成的角，
由题意知∠BAC=90°，∠ACB=45°，
∴△ABC为等腰直角三角形，
且AB=AC=2，∴BO=
| 5 |
在Rt△SBO中，SB=
| SO2+BO2 |
| 2 |
∴cos∠SBO=
| ||
2
|
| ||
| 4 |
∴二面角A-SB-C的余弦值为
| ||
| 4 |
点评：本题考查异面直线垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意空间思维能力的合理运用．
练习册系列答案
相关题目
圆的圆心，E为BC的中点．