Question

图一是由三个边长均为2的正三角形和一个半圆及一个扇形组成的平面图形，将其折起恰好围成如图二所示的几何体，在该几何体中，点O为半圆的圆心，E为BC的中点．
（1）求证：BC⊥平面ADE；
（2）求图二所示几何体的体积；
（3）求二面角A-BC-E的余弦值．

Answer 1

考点：二面角的平面角及求法,直线与平面垂直的性质

专题：空间位置关系与距离,空间角

分析：（1）连接OA，OD，OE，由已知条件推导出BC⊥OE，BC⊥OD，从而BC⊥平面ODE，进而BC⊥DE，同理可证BC⊥AD，由此能证明BC⊥平面ADE．
（Ⅱ）由题意知三棱锥D-ABC为棱长是2的正四面体，作DH⊥平面ABC于点H，由点H为△ABC的重心，AH=

2

3

AO=

2

3

AB2-OB2

=

2 3

3

，图二所示几何体是由正四面体和半圆锥组成的，由此能求出该几何体的体积．
（Ⅲ）二面角A-BC-E的大小等于二面角A-BC-D和二面角D-BC-E的大小的和，由此能求出二面角A-BC-E的余弦值．

解答： （1）证明：连接OA，OD，OE，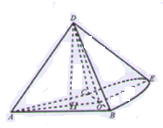
∵O为半圆圆心，E为BC中点，∴BC⊥OE，
∵BD=CD，OB=OC，∴BC⊥OD，
∵OE，OD?平面ODE，且OD∩OE=O，
∴BC⊥平面ODE，又DE?平面ODE，
∴BC⊥DE，同理可证BC⊥AD，
∵AD∩DE=D，且AD，DE⊆平面ADE，
∴BC⊥平面ADE．
（Ⅱ）解：由题意知三棱锥D-ABC为棱长是2的正四面体，
作DH⊥平面ABC于点H，由点H为△ABC的重心，
∴AH=

2

3

AO=

2

3

AB2-OB2

=

2 3

3

，
在Rt△DAH中，DH=

DA2-AH2

=

22-( 2 3 3 )2

=

2 6

3

，
∵S△ABC=

3

4

×22=

3

，
∴VD-ABC=

1

3

•S△ABC•DH=

3

3

×

2 6

3

=

2 2

3

，
由题意知D-BEC为半圆锥，且其高OD=

DB2-OB2

=

3

，
底面半径OB=1，
∴V_半圆锥=

1

2

×(

1

3

π•OB2•OD)=

3 π

6

，
∵该几何体是由正四面体和半圆锥组成的，所以该几何体的体积为：
V=

2 2

3

+

3 π

6

．
（Ⅲ）解：二面角A-BC-E的大小等于二面角A-BC-D和二面角D-BC-E的大小的和，
且由（1）知∠AOD，∠DOE分别是二面角A-BC-D和二面角D-BC-E的平面角，
由题意知∠DOE=

π

2

，在Rt△HOD中，sin∠AOD=

DH

OD

=

2 2

3

，
∴二面角A-BC-E的余弦值为cos（

π

2

+∠AOD）=-sin∠AOD=-

2 2

3

．

点评：本题考查直线与平面垂直的证明，考查几何体的体积的求法，考查二面角的余弦值的求法，解题时要认真审题，注意空间思维能力的培养．