题目内容

设O为原点，点M在圆C2：x2+y2+4x-4y=0上运动，则|OM|的最大值为
 
．
考点：圆的一般方程
专题：直线与圆
分析：先求出圆心和半径r，再求得|C2O|=2
2
，则|OM|的最大值为|C2O|+r．
解答： 解：圆C2：x2+y2+4x-4y=0，即 （x+2）2+（y-2）2=8，表示以C2（-2，2）为圆心，半径r等于2
2
的圆．
由于|C2O|=2
2
，∴|OM|的最大值为|C2O|+r=4
4
，
故答案为：4
2
．
点评：本题主要考查圆的一般方程，点与圆的位置关系，属于中档题．
练习册系列答案
相关题目
已知命题p：直线y=x+t与抛物线y2=4x有两个交点；命题q：关于x的方程x2-tx+4=0有实根．若p∨q为真命题，p∧q为假命题，求实数t的取值范围．
在△ABC中，已知角A、B、C的对边分别为a、b、c，向量
m
=（a+c，a-b），
n
=（sinB，sinA-sinC），且
m
∥
n
，
（1）求∠C的大小；
（2）求sinA+sinB的取值范围．
已知抛物线C：x2=2py（p＞0）的焦点为F，准线为l，A为抛物线C上一点，已知以F为圆心，FA为半径的圆F交于B、D两点．
（Ⅰ）若∠BFD=90°，且△BFD的面积为4，求p的值及圆F的方程；
（Ⅱ）若A、B、F三点在同一直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到m、n距离的比值．
给出下列五个命题：
①函数y=2sin（2x-
π
3
）的一条对称轴是x=
5π
12
；
②函数y=tan2x的图象关于点（
π
4
，0）对称；
③正弦函数在第一象限为增函数；
④若锐角α终边上一点的坐标为（2sin3，-2cos3），则α=3-
π
2
；
⑤函数f（x）=x-sinx有3个零点；
以上五个命题中正确的有
 
（填写正确命题前面的序号）．
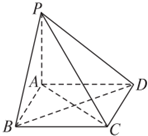已知PA垂直于正方形ABCD所在平面，连接PB、PC、PD、AC、BD，则下列垂直关系中正确的序号是
 
．
①平面PAB⊥平面PBC  
②平面PAB⊥平面PAD
③平面PAB⊥平面PCD．
已知直线
2a
x+
b
y=1（其中a，b为正实数）与圆x2+y2=1相相交于A，B两点，O为坐标原点，且△AOB为直角三角形，则a2+b2-2（a+b）取值范围为
 
．
一种专门占据内存的计算机病毒开始时占据内存2KB，然后每3分钟自身复制一次，复制后所占内存是原来的2倍，那么开机后
 
分钟，该病毒占据内存32MB（1MB=210KB）．
下列说法：
①设α，β都是锐角，则必有sin（α+β）＜sinα+sinβ
②在△ABC中，若sin2A+sin2B＜sin2C，则△ABC为锐角三角形．
③在△ABC中，若A＜B，则cos2A＜cos2B；
则其中正确命题的序号是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网