题目内容
 2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达3.32亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为0.4.
2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达3.32亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为0.4.| 网购金额(元) | 频数 | 频率 |
| (0,500] | 5 | 0.05 |
| (500,1000] | x | p |
| (1000,1500] | 15 | 0.15 |
| (1500,2000] | 25 | 0.25 |
| (2000,2500] | 30 | 0.3 |
| (2500,3000] | y | q |
| 合计 | 100 | 1.00 |
(Ⅱ)为进一步了解网购金额的多少是否与网龄有关,对这100名网购者调查显示:购物金额在2000元以上的网购者中网龄3年以上的有35人,购物金额在2000元以下(含2000元)的网购者中网龄不足3年的有20人.
①请将列联表补充完整;
| 网龄3年以上 | 网龄不足3年 | 合计 | |
| 购物金额在2000元以上 | 35 | ||
| 购物金额在2000元以下 | 20 | ||
| 合计 | 100 |
参考数据:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
考点:独立性检验
专题:应用题,概率与统计
分析:(1)求出网购金额在2000元以上的人数,可得x,y的值,由此能求出x,y,p,q的值,并补全频率分布直方图.
(2)由数据可得列联表,利用公式,可得结论.
(2)由数据可得列联表,利用公式,可得结论.
解答:
 解:(1)因为网购金额在2000元以上的频率为0.4,
解:(1)因为网购金额在2000元以上的频率为0.4,
所以网购金额在2000元以上的人数为100×0.4=40
所以30+y=40,
所以y=10,…(1分)
x=15,…(2分)
所以p=0.15,q=0.1…(4分)
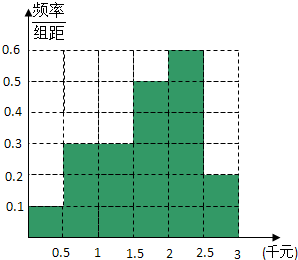
所以频率分布直方图如右图…(5分)
(2)由题设列联表如下
…(7分)
所以K2=
≈5.56>5.024…(10分)
所以据此列联表判断,有97.5%的把握认为网购金额超过2000元与网龄在三年以上有关.…(12分)
 解:(1)因为网购金额在2000元以上的频率为0.4,
解:(1)因为网购金额在2000元以上的频率为0.4,所以网购金额在2000元以上的人数为100×0.4=40
所以30+y=40,
所以y=10,…(1分)
x=15,…(2分)
所以p=0.15,q=0.1…(4分)
所以频率分布直方图如右图…(5分)
(2)由题设列联表如下
| 网龄3年以上 | 网龄不足3年 | 合计 | |
| 购物金额在2000元以上 | 35 | 5 | 40 |
| 购物金额在2000元以下 | 40 | 20 | 60 |
| 合计 | 75 | 25 | 100 |
所以K2=
| 100×(35×20-40×5)2 |
| 75×25×40×60 |
所以据此列联表判断,有97.5%的把握认为网购金额超过2000元与网龄在三年以上有关.…(12分)
点评:本题考查频率分布直方图,考查独立性检验的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知i是虚数单位,若复数z满足(z-i)(3-i)=10,则复数z所对应的点位于复平面的( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若函数f(x)=x3-3ax+3a在区间(0,2)内有极小值,则a的取值范围是( )
| A、a>0 | B、a>2 |
| C、0<a<2 | D、0<a<4 |
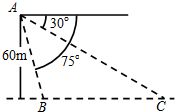 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60m,则河流的宽度BC等于( )
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60m,则河流的宽度BC等于( )A、30(
| ||
B、120(
| ||
C、180(
| ||
D、240(
|