题目内容
已知
=3+2
,求cos2(π-α)+sin(π+α)cos(π-α)+2sin2(π-α)的值.
| 1+tanα |
| 1-tanα |
| 2 |
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:三角函数的求值
分析:由条件求得tanα的值,再利用同角三角函数的基本关系、诱导公式化简所给的式子,可得结果.
解答:
解:∵
=3+2
,
∴tanα=
=
,
∴cos2(π-α)+sin(π+α)cos(π-α)+2sin2(π-α)=cos2α+sinαcosα+2sin2α=
=
=
=
.
| 1+tanα |
| 1-tanα |
| 2 |
∴tanα=
1+
| ||
2+
|
| 2 |
∴cos2(π-α)+sin(π+α)cos(π-α)+2sin2(π-α)=cos2α+sinαcosα+2sin2α=
| cos2α+sinαcosα+2sin2α |
| sin2α+cos2α |
=
| 1+tanα+2tan2α |
| tan2α+1 |
1+
| ||
| 2+1 |
5+
| ||
| 3 |
点评:本题主要考查同角三角函数的基本关系、诱导公式的应用,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
经过双曲线
-
=1(a>b>0)的右焦点为F作该双曲线一条渐近线的垂线与两条渐近线相交于M,N两点,若O是坐标原点,△OMN的面积是
a2,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
已知抛物线y2=4x与双曲线
-
=1(a>0,b>0)有相同的焦点F,点A,B是两曲线的交点,若(
+
)•
=0,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| OA |
| OB |
| AF |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知A、B、C为三个不共线的点,P为△ABC所在平面内一点,若
+
=
+
,则点P与△ABC的位置关系是( )
| PA |
| PB |
| PC |
| AB |
| A、点P在△ABC内部 |
| B、点P在△ABC外部 |
| C、点P在直线AB上 |
| D、点P在直线AC上 |
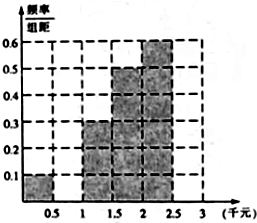 2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达3.32亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为0.4.
2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达3.32亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为0.4.