题目内容

已知数列{an}满足a1=0，an+1=
1+an
3-an
，写出若干项，并归纳通项公式an=
 
．
考点：归纳推理,数列递推式
专题：计算题,等差数列与等比数列
分析：利用数列递推式，代入计算，可得这个数列的前5项并归纳通项公式．
解答： 解：a1=0=
0
2
，a2=
1
3
，a3=
1
2
=
2
4
，a4=
3
5
，a5=
2
3
=
4
6
，归纳通项公式an=
n-1
n+1

故答案为：
n-1
n+1
．
点评：本题考查数列递推式，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知A（0，1），B（4，t），是否存在实数t，满足A，B两点作与x轴相切的圆有且只有一个？若存在满足条件的圆，求出这个圆的方程；若不存在满足条件的圆，请说明理由．
“x＜1”是“log2（x+1）＜1”的（　　）
A、充分而不必要条件
B、必要而不充分条件
C、充要条件
D、既不充分也不必要条件
抛物线C1：y2=4x，双曲线C2：
x2
a2
-
y2
b2
=1（a＞0，b＞0），若C1的焦点恰为C2的右焦点，则2a+b的最大值为（　　）
A、
5
B、5
C、
2
D、2
已知抛物线y2=4x与双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）有相同的焦点F，点A，B是两曲线的交点，若（
OA
+
OB
）•
AF
=0，则双曲线的离心率为（　　）
A、
2
+2
B、
5
+1
C、
3
+1
D、
2
+1
已知数列：2×
1
2
，3×
1
4
，4×
1
8
，5×
1
16
…（n+1）×
1
2n
，求数列的前n项和Sn．
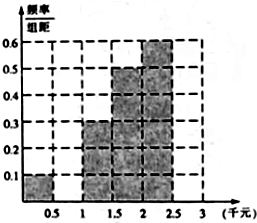2014年7月16日，中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》，报告显示：我国网络购物用户已达3.32亿．为了了解网购者一次性购物金额情况，某统计部门随机抽查了6月1日这一天100名网购者的网购情况，得到如下数据统计表．已知网购金额在2000元以上（不含2000元）的频率为0.4．
网购金额（元）频数频率
（0，500]50.05
（500，1000]xp
（1000，1500]150.15
（1500，2000]250.25
（2000，2500]300.3
（2500，3000]yq
合计1001.00
（Ⅰ）确定x，y，p，q的值，并补全频率分布直方图；
（Ⅱ）为进一步了解网购金额的多少是否与网龄有关，对这100名网购者调查显示：购物金额在2000元以上的网购者中网龄3年以上的有35人，购物金额在2000元以下（含2000元）的网购者中网龄不足3年的有20人．
①请将列联表补充完整；
网龄3年以上网龄不足3年合计
购物金额在2000元以上35
购物金额在2000元以下20
合计100
②并据此列联表判断，是否有97.5%的把握认为网购金额超过2000元与网龄在三年以上有关？
参考数据：
P（K2≥k）0.150.100.050.0250.0100.0050.001
k2.0722.7063.8415.0246.6357.87910.828
（参考公式：K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
，其中n=a+b+c+d）
函数y=
sinx
+
-cosx
的定义域是（　　）
A、[kπ+
π
2
，（2k+1）π]（k∈Z）
B、[kπ+
π
2
，（k+1）π]（k∈Z）
C、[2kπ+
π
2
，（2k+1）π]（k∈Z）
D、[2kπ，（2k+1）π]（k∈Z）
在一次“爱眼日”活动中，随机抽取高三（1）班6名男生和6名女生的视力数据制成茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶）：视力为5.0（含5.0）以上为正常视力，其他为近视眼．
（1）若该班有50人，用样本数据估计全班同学的平均视力和有多少人近视？
（2）为了进一步了解近视的成因、从男、女两组中随机各选取一名已得近视的同学的视力数据，记为x，y，求事件“|x-y|≤0.1”的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网