题目内容
14.已知实数x,y满足条件$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\\{x+y≤3}\end{array}\right.$,则z=2x+y+3的最大值是( )| A. | 3 | B. | 5 | C. | 7 | D. | 8 |
分析 画出约束条件的可行域,利用目标函数的几何意义求解最大值即可.
解答  解:实数x,y满足条件$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\\{x+y≤3}\end{array}\right.$,满足的可行域如图:
解:实数x,y满足条件$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\\{x+y≤3}\end{array}\right.$,满足的可行域如图:
则z=2x+y+3即y=-2x+z-3,平移直线y=-2x+z-3,当直线y=-2x+z-3经过A时,目标函数取得最大值.
由$\left\{\begin{array}{l}{x=2}\\{x+y=3}\end{array}\right.$,可得A(2,1),
则z=2x+y+3的最大值是:2×2+1+3=8.
故选:D.
点评 本题考查线性规划的简单应用,画出可行域,判断目标函数的最值是解题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
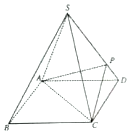 如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,点P在侧棱SD上,且SP=3PD.
如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,点P在侧棱SD上,且SP=3PD. 如图,正八面体P-ABCD-Q由两个棱长都为a的正四棱锥拼接而成.
如图,正八面体P-ABCD-Q由两个棱长都为a的正四棱锥拼接而成.