题目内容
1.已知圆C1:(x-1)2+y2=$\frac{1}{2}$与圆C2的公切线是直线y=x和y=-x,且两圆的圆心距是3,求圆C2的方程.分析 由题意,圆C2的圆心C2在x轴或y轴上,分类讨论,求出圆心与半径,即可得出结论.
解答 解:由题意,圆C2的圆心C2在x轴或y轴上,
①设C2(a,0),则|a-1|=3,a=4或-2,
(4,0)到直线y=x的距离是$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$,(-2,0)到直线y=x的距离是$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
∴圆C2的方程是:(x-4)2+y2=8或:(x+2)2+y2=2;
②设C2(0,b),则$\sqrt{1+{b}^{2}}$=3,∴b=$±2\sqrt{2}$,
(0,$±2\sqrt{2}$)到直线y=x的距离是$\frac{2\sqrt{2}}{\sqrt{2}}$=2,
∴圆C2的方程是:x2+(y-2$\sqrt{2}$)2=4或x2+(y+2$\sqrt{2}$)2=4.
点评 本题考查圆的方程,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
11.已知$f(x)=sin(ωx+ϕ)(ω>0,|ϕ|<\frac{π}{2})$的最小正周期为π,若其图象向左平移$\frac{π}{3}$个单位后关于y轴对称,则( )
| A. | $ω=2,ϕ=\frac{π}{3}$ | B. | $ω=2,ϕ=\frac{π}{6}$ | C. | $ω=4,ϕ=\frac{π}{6}$ | D. | $ω=2,ϕ=-\frac{π}{6}$ |
12.已知函数f(x)是定义域为R的奇函数,且当x<0时xf'(x)+f(x)<0,记a=3f(3),b=f(sin1)sin1,c=-2$\sqrt{2}f(-2\sqrt{2})$,则a,b,c的大小关系式( )
| A. | a>c>b | B. | c>a>b | C. | c>b>a | D. | a>b>c |
16.已知点P在以点F1,F2分别为左、右焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,且满足$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0,tan∠PF1F2=$\frac{1}{3}$,则该双曲线的离心率是( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{10}}{2}$ |
10.已知a∈R,则“a>3”是“a2>2a+3”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
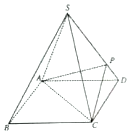 如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,点P在侧棱SD上,且SP=3PD.
如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,点P在侧棱SD上,且SP=3PD.