题目内容
17．一海豚在水池中（不考虑水的深度）自由游戏，已知水池的长为30m，宽为20m，则海豚嘴尖离池边超过4m的概率为$\frac{11}{25}$．分析 测度为面积，找出点离岸边不超过4m的点对应的图形的面积，并将其和长方形面积一齐代入几何概型计算公式进行求解．
解答 解：如图所示：
长方形面积为20×30，小长方形面积为22×12，
阴影部分的面积为20×30-22×12，
∴海豚嘴尖离岸边不超过2m的概率为P=1-$\frac{22×12}{20×30}$=$\frac{11}{25}$．
故答案为$\frac{11}{25}$．
点评 本题考查几何概型，明确测度，正确求解面积是关键．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
7．对于常数m、n，“mn＜0”是“方程mx2+ny2=10的曲线是双曲线”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
8．
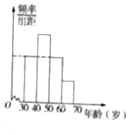韩国民意调查机构“盖洛普韩国”2016年11月公布的民调结果显示，受“闺蜜门”时间影响，韩国总统朴槿惠的民意支持率持续下跌，在所调查的1000个对象中，年龄在[20，30）的群体有200人，支持率为0%，年龄在[30，40）和[40，50）的群体中，支持率均为3%；年龄在[50，60）和[60，70）的群体中，支持率分别为6%和13%，若在调查的对象中，除[20，30）的群体外，其余各年龄层的人数分布情况如频率分布直方图所示，其中最后三组的频数构成公差为100的等差数列．
（1）依频率分布直方图求出图中各年龄层的人数
（2）请依上述支持率完成下表：
根据表中的数据，能否在犯错误的概率不超过0.001的前提下认为年龄与支持率有关？
附表：
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d 参考数据：125×33=15×275，125×97=25×485）
韩国民意调查机构“盖洛普韩国”2016年11月公布的民调结果显示，受“闺蜜门”时间影响，韩国总统朴槿惠的民意支持率持续下跌，在所调查的1000个对象中，年龄在[20，30）的群体有200人，支持率为0%，年龄在[30，40）和[40，50）的群体中，支持率均为3%；年龄在[50，60）和[60，70）的群体中，支持率分别为6%和13%，若在调查的对象中，除[20，30）的群体外，其余各年龄层的人数分布情况如频率分布直方图所示，其中最后三组的频数构成公差为100的等差数列．（1）依频率分布直方图求出图中各年龄层的人数
（2）请依上述支持率完成下表：
| 年龄分布 是否支持 | [30，40）和[40，50） | [50，60）和[60，70） | 合计 |
| 支持 | 15 | 25 | 40 |
| 不支持 | 485 | 275 | 760 |
| 合计 | 500 | 300 | 800 |
附表：
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
12．已知函数f（x）是定义域为R的奇函数，且当x＜0时xf'（x）+f（x）＜0，记a=3f（3），b=f（sin1）sin1，c=-2$\sqrt{2}f（-2\sqrt{2}）$，则a，b，c的大小关系式（ ）
| A． | a＞c＞b | B． | c＞a＞b | C． | c＞b＞a | D． | a＞b＞c |
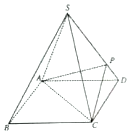如图所示，四棱锥S-ABCD的底面是正方形，每条侧棱的长都是底面边长的$\sqrt{2}$倍，点P在侧棱SD上，且SP=3PD．