题目内容
15.已知p:|3x-4|>2,$q:\frac{1}{{{x^2}-x-2}}$>0,r:(x-a)(x-a-1)<0,(1)?p是?q的什么条件?
(2)若?r是?p的必要非充分条件,试求实数a的取值范围.
分析 (1)求出命题p,q的等价条件,根据充分条件和必要条件的定义进行判断即可.
(2)根据¬r是¬p的必要非充分条件,进行转化,建立不等式关系进行求解即可.
解答 解:(1)由|3x-4|>2得3x-4>2或3x-4<-2,
即x>2或x<$\frac{2}{3}$,即p:x>2或x<$\frac{2}{3}$,¬p:$\frac{2}{3}$≤x≤2
由$q:\frac{1}{{{x^2}-x-2}}$>0得x2-x-2>0得x>2或x<-1,即:¬q:-1≤x≤2,
则¬p是¬q的充分不必要条件.
(2)由(x-a)(x-a-1)<0得a<x<a+1,即r:a<x<a+1,
若¬r是¬p的必要非充分条件,
则p是r的必要非充分条件,
即a≥2或a+1≤$\frac{2}{3}$,
即a≥2或a≤-$\frac{1}{3}$,
即实数a的取值范围是a≥2或a≤-$\frac{1}{3}$.
点评 本题主要考查充分条件和必要条件的判断和应用,根据充分条件和必要条件的定义进行转化是解决本题的关键.

练习册系列答案
相关题目
5.已知函数f(x)是定义在R上的偶函数,当x∈[0,+∞)时,f(x)是增函数,且f(-1)=0则不等式f(x)<0的解集为( )
| A. | (-1,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-∞,-1)∪(0,1) | D. | (-1,0)∪(0,1) |
6.某程序框图如图所示,执行该程序,若输入的a值为1,则输出的a值为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
10.若两条直线ax+2y+6=0与x+(a-1)y+(a2-1)=0平行,则a的取值集合是( )
| A. | {-1,2} | B. | {-1} | C. | {2} | D. | $\left\{{\frac{2}{3}}\right\}$ |
20.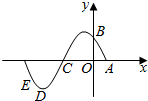 已知A,B,C,D是函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)一个周期内的图象上的四个点,如图所示,$A(\frac{π}{6},0)$,B为y轴上的点,D为图象上的最低点,C为该函数图象的一个对称中心,B与E关于点C对称,$\overrightarrow{ED}$在x轴上的投影为$\frac{π}{12}$,则$f(-\frac{π}{6})$的值为( )
已知A,B,C,D是函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)一个周期内的图象上的四个点,如图所示,$A(\frac{π}{6},0)$,B为y轴上的点,D为图象上的最低点,C为该函数图象的一个对称中心,B与E关于点C对称,$\overrightarrow{ED}$在x轴上的投影为$\frac{π}{12}$,则$f(-\frac{π}{6})$的值为( )
 已知A,B,C,D是函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)一个周期内的图象上的四个点,如图所示,$A(\frac{π}{6},0)$,B为y轴上的点,D为图象上的最低点,C为该函数图象的一个对称中心,B与E关于点C对称,$\overrightarrow{ED}$在x轴上的投影为$\frac{π}{12}$,则$f(-\frac{π}{6})$的值为( )
已知A,B,C,D是函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)一个周期内的图象上的四个点,如图所示,$A(\frac{π}{6},0)$,B为y轴上的点,D为图象上的最低点,C为该函数图象的一个对称中心,B与E关于点C对称,$\overrightarrow{ED}$在x轴上的投影为$\frac{π}{12}$,则$f(-\frac{π}{6})$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
4.已知m,n表示两条不同的直线,α,β表示两个不同的平面,且m?α,n?β,则下列说法正确的是( )
| A. | 若α∥β,则m∥n | B. | 若m⊥β,则α⊥β | C. | 若m∥β,则α∥β | D. | 若α⊥β,则m⊥n |